Пример 19.1. Введем в ячейки такие значения (рис. 19.1).
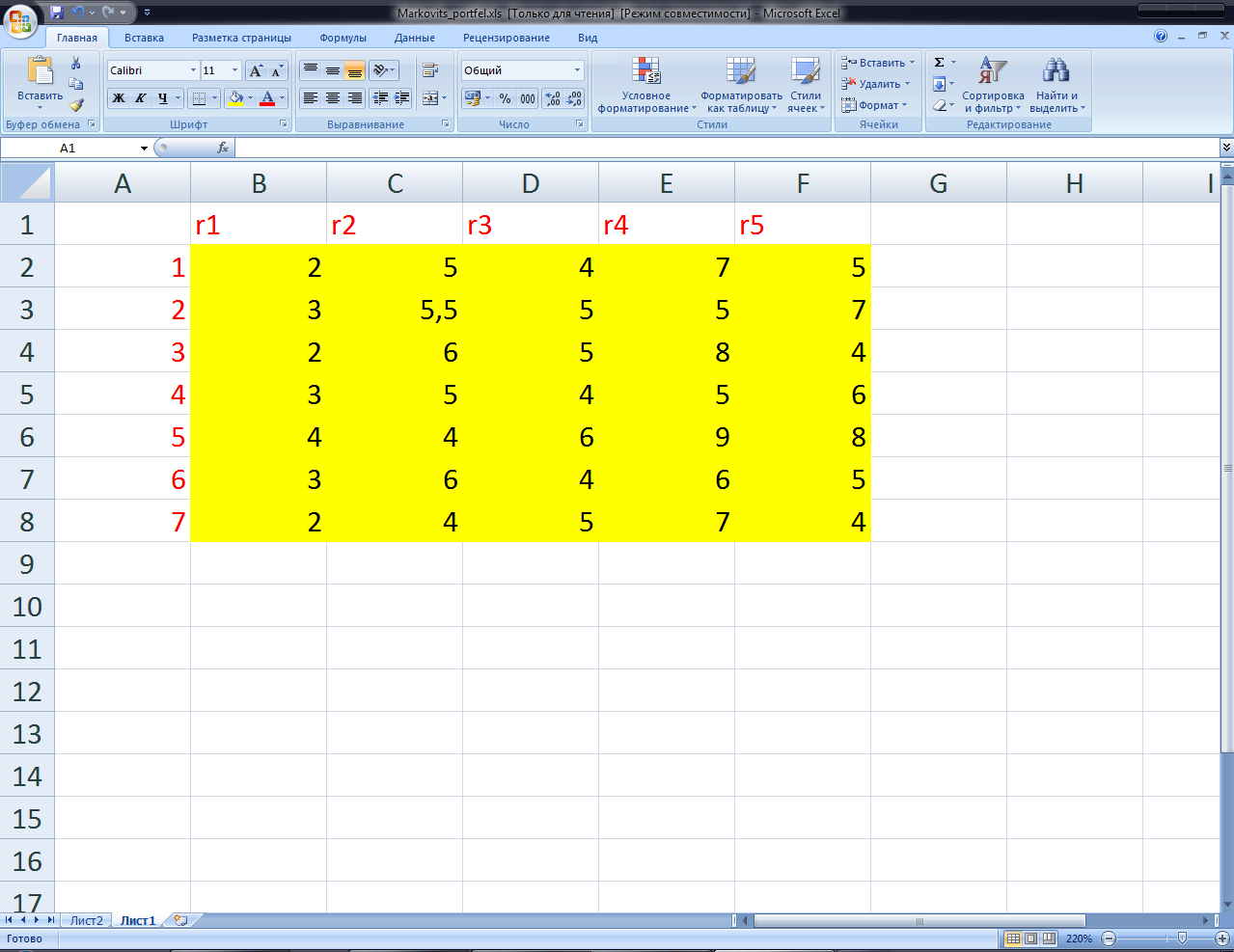
Рис. 19.1. Ввод данных
Находим среднее значение для ячейки В9: открываем Мастер функций. Для этого определяем курсором ячейку В9, щелкаем мышью на кнопке  в строке состояния и открывается окно Мастер функций. В категории выбираем Статистические, в перечне функций находим функцию СРЗНАЧи нажимаем ОК(Рис. 19.2; 19.3).
в строке состояния и открывается окно Мастер функций. В категории выбираем Статистические, в перечне функций находим функцию СРЗНАЧи нажимаем ОК(Рис. 19.2; 19.3).
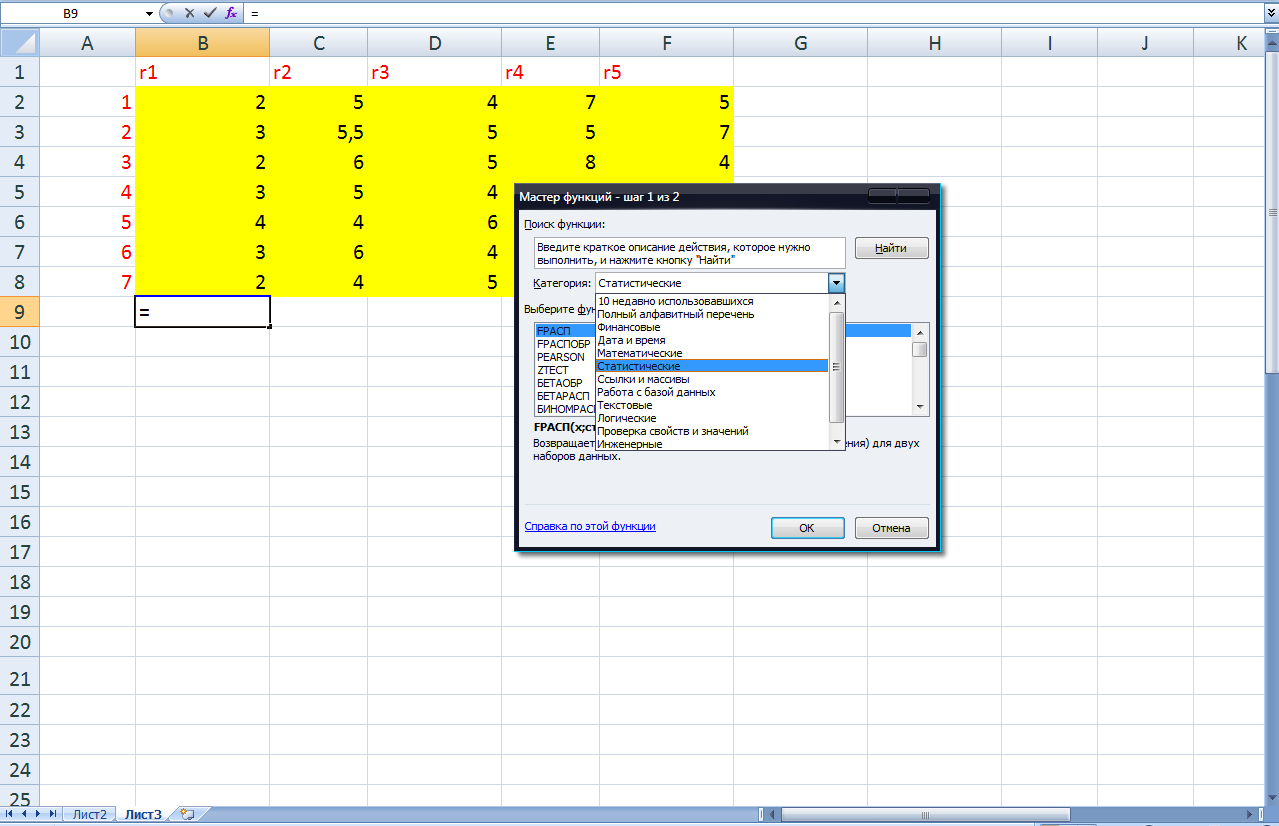
Рис. 19.2. Выбор категории

Рис. 19.3. Выбор функции СРЗНАЧ
В появившемся диалоговом окне Аргументы функцииопределяем массив В2:В8 и нажимаем ОК (Рис.19. 4).

Рис. 19.4 Выбор массива
В нашем примере среднее значение = 2,714. Чтобы посчитать среднее значение r2,r3,r4,r5, мы направляем курсор в правый нижний угол на ячейку В9 (нажимаем) и тянем до ячейки F9 (включительно) (рис 19.5).

Рис. 19.5 Расчет среднего значения для r2,r3,r4,r5.
Аналогичным способом вычисляем КОВАРИАЦИЮ. Определяем курсором ячейку В11, затем открываем, мастер функций, в перечне функций находим функцию КОВАРи нажимаем ОК. При выборе массива 1вводим $B2:$B8, массив 2 – B$2:B$8 (рис. 19.6). После этого нажимаем ОК, и полученное в ячейке В11 протягиваем до ячейки F11(вкл-но) (рис. 19.7).

Рис.19.6 Выбор массива

Рис. 19.7 Расчет ковариации
Расчет ковариации для 2 и Н делаем все аналогичным способом, только массив 1- $C2:$C8, массив 2- В$2:В$8. Для 3 и Н используем массив 1 - $D2:$D8. 4 и Н массив 1 -$E2:$E8, 5 и Н массив 1 - $F2:$F8 (массив 2 - у всех одинаковый) (рис.16.8).

Рис. 19.8 Расчет ковариации
После этого составляем матрицу A, направляем курсор на В18 и в строку формул вводим: =2*В11; для C19: =2*C12; D20: =2*D13; E21=2*E14; F22: =2*F15, а L2- среднее значение (рис. 19.9).

Рис. 19.9 Составление матрицы
Матрица обратная  . Для этого определяем курсором ячейку В26, щелкаем мышью на кнопке
. Для этого определяем курсором ячейку В26, щелкаем мышью на кнопке  в строке состояния и открывается окно Мастер функций. В категории выбираем Математические, в перечне функций находим функцию МОБР(находит матрицу, обратную к данной)и нажимаем ОК.В массив вводим: B18:H24, нажимаем ок. Полученное значение: 0,187. Чтобы виден был весь ответ, выполняем следующие действия: Начиная с ячейки B26 выделяем семь строк и семь столбцов (именно столько было у исходной матрицы и столько же будет у обратной), нажимаем клавишу F2, а затем одновременно на три клавиши Ctrl+Shift+Enter. В выделенном месте появляются, теперь уже все, элементы обратной матрицы (рис. 19.10).
в строке состояния и открывается окно Мастер функций. В категории выбираем Математические, в перечне функций находим функцию МОБР(находит матрицу, обратную к данной)и нажимаем ОК.В массив вводим: B18:H24, нажимаем ок. Полученное значение: 0,187. Чтобы виден был весь ответ, выполняем следующие действия: Начиная с ячейки B26 выделяем семь строк и семь столбцов (именно столько было у исходной матрицы и столько же будет у обратной), нажимаем клавишу F2, а затем одновременно на три клавиши Ctrl+Shift+Enter. В выделенном месте появляются, теперь уже все, элементы обратной матрицы (рис. 19.10).

Рис. 19.10 Обратная матрица
Находим произведение двух матриц. Определяем курсором ячейку J26, щелкаем мышью на кнопке  в строке состояния и открывается окно Мастер функций. В категории оставляем Математические, в перечне функций находим функцию МУМНОЖи нажимаем ОК. В массив 1 вводим: B26:H32, а в массив 2: N18:N24, и нажимаем ок. Полученное значение: 0,079. Чтобы виден был весь ответ, выделяем семь строк, начиная с ячейки J26. Нажимаем клавишу F2, а затем одновременно на три клавиши Ctrl+Shift+Enter. В выделенном месте появляются, теперь уже все значения. После этого считаем сумму этих значений в ячейке J33 (функцию выбираем СУММ) и нажимаем ок. В число 1 записываем J26:J32, нажимаем ок (рис.19.11).
в строке состояния и открывается окно Мастер функций. В категории оставляем Математические, в перечне функций находим функцию МУМНОЖи нажимаем ОК. В массив 1 вводим: B26:H32, а в массив 2: N18:N24, и нажимаем ок. Полученное значение: 0,079. Чтобы виден был весь ответ, выделяем семь строк, начиная с ячейки J26. Нажимаем клавишу F2, а затем одновременно на три клавиши Ctrl+Shift+Enter. В выделенном месте появляются, теперь уже все значения. После этого считаем сумму этих значений в ячейке J33 (функцию выбираем СУММ) и нажимаем ок. В число 1 записываем J26:J32, нажимаем ок (рис.19.11).

Рис. 19.11 Произведение двух матриц
Теперь переносим полученные значения с J26-J30 в K26-K30, и считаем сумму для этих значений. Ответ получается: 1,000. После этого значения J26-J30 возводим в квадрат, определяем курсором ячейку L26, щелкаем мышью на кнопке  в строке состояния и открывается окно Мастер функций. Категория остается математические, функцию выбираем – СТЕПЕНЬ и нажимаем ок. А окне аргументы функций, там где число вбиваем К26, а там где степеньвбиваем 2. Ответ получился 0,006. Протягием эту ячейку до L30(включительно) (рис.19.12). Как видно на рис. 19.12 заданная доходность равна 5% (М26).
в строке состояния и открывается окно Мастер функций. Категория остается математические, функцию выбираем – СТЕПЕНЬ и нажимаем ок. А окне аргументы функций, там где число вбиваем К26, а там где степеньвбиваем 2. Ответ получился 0,006. Протягием эту ячейку до L30(включительно) (рис.19.12). Как видно на рис. 19.12 заданная доходность равна 5% (М26).

Рис. 19.12 Возведение в квадрат
Теперь находим Матрицу А1 единичную. Для этого определяем курсором В34, открываем мастер функций, выбираем функцию МУМНОЖ, и нажимаем ОК. МАССИВ 1= (B18:H24), МАССИВ 2 = (В26:H32) и нажимаем ок, полученное значение = Чтобы виден был весь ответ, выделяем аналогично предыдущей матрицы кол-во ячеек. Нажимаем клавишу F2, а затем одновременно на три клавиши Ctrl+Shift+Enter. В выделенном месте появляются, теперь уже все значения (рис. 19.13).

Рис. 19.13 Выбор массива для матрицы единичной
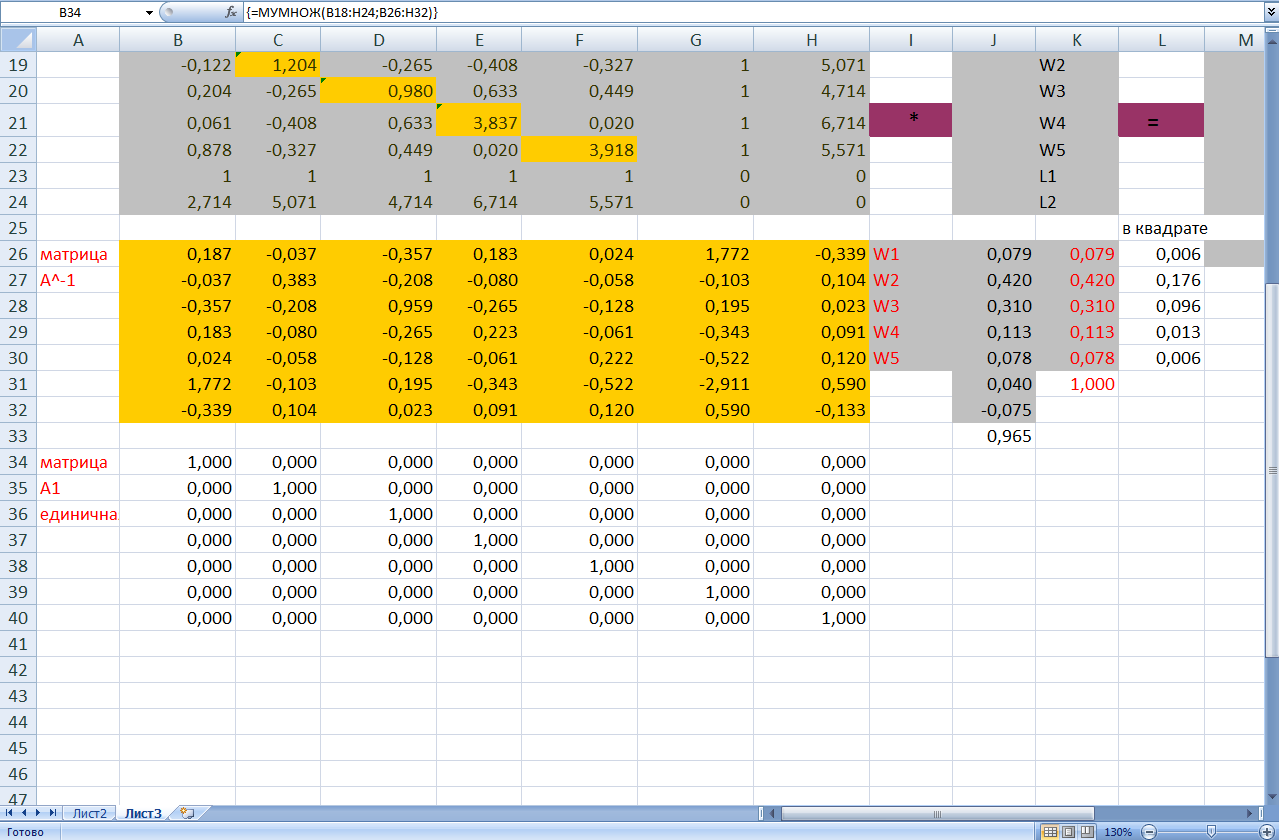
Рис. 19.14 Единичная матрица
После того как нашли единичную матрицу рассчитываем дисперсию r1, r2, r3, r4, r5. Для этого определяем курсором ячейку L36, выбираем категорию СТАТИСТИЧЕСКИЕ, функцию – ДИСПР, а массив В2:В8, и нажимаем ок (протягиваем L36 до Р36) (рис. 19.15).

Рис 19.15. Расчет дисперсии
Дисперсию Портфеля мы находим через мастер функций, категорию выбираем математические, функцию – ДИСПР, массив 1- L36:P36, массив 2 – L26:L30, а курсором определяем ячейку L37 (рис. 19.16). Дисперсия портфеля равна 0,192785.

Рис. 19.16 Дисперсия Портфеля
Находим ковариацию на примере ячейки L40. В строку формул вводим =$J27*B12 и получаем значение -0,051. Протягиваем эту ячейку для всех r1-r5 (рис. 19.17)

Рис. 19.17 Расчет ковариации
После расчета ковариации, считаем сумму для r1- r5. Для этого определяем курсором ячейку L44, открываем мастер функций, выбираем функцию СУММ, нажимаем Ок, пишем в массив L39:L4, нажимаем ОК. Тянем ячейку L44 до Р44 (рис.19.18).

Рис. 19.18 Расчет суммы для r1-r5
Теперь посчитаем сумму для 1и Н – 5 и Н. Для этого определяем курсором ячейку Q39, нажимаем мастер функций, выбираем функцию СУММ, нажимаем ОК. Массив вводим L39:P39, нажимаем ок. Полученное значение = 0,080, протягиваем эту ячейку до Q44 (включительно) (рис. 19.19).

Рис. 19.19. Расчет суммы для 1 и Н – 5 и Н.
Рассчитываем ковариацию ху. н. Определяем курсором ячейку L45, открываем мастер функций, выбираем категорию математические, а функцию МУМНОЖ. В массив вводим L44:P44 и K26:K30,нажимаем ОК. Полученный ответ = -0, 0490. А дисперсию находим через функцию МУМНОЖ, в массив 1 вводим L36:P36, в массив 2 вводим L26:L30, нажимаем ОК. После этого в строку формул добавляем к главной формуле +L45 и нажимаем ENTER. В ячейке L46 получаем значение: 0,1438 (рис.19.20).
Для расчета сигмы происходит через мастер функций, функция КОРЕНЬ, а Число мы выбираем L46 и нажимаем ОК. Полученное значение
= 0,3792 (рис. 19.21).

Рис. 19.20 Расчет дисперсии

Рис. 19.21 Расчет сигмы
По правилу теперь умножаем нашу сигму на 3 и -3. Для этого определяем курсором ячейку L48, а в строке формул пишем =3*L47 и для ячейки L49 пишем в строке формул =-3*L47 (рис. 19.22).
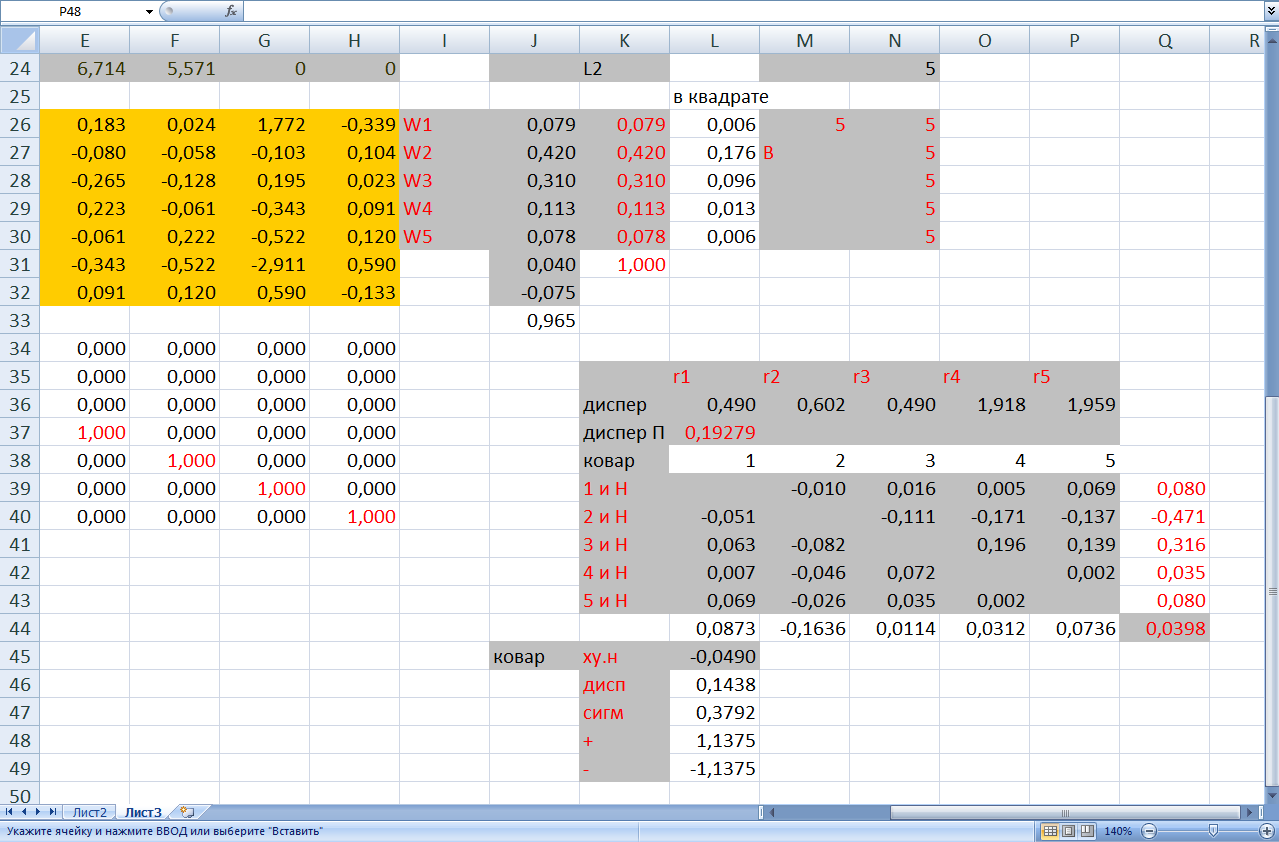
Рис. 19.22 Правило 3-х s (трех “сигм”)
Инвестиционный портфель Марковица в Excel выглядит таким образом (рис. 19.23).

Рис. 19.23 Инвестиционный портфель Марковица
Вопросы и задачи к теме
Вопросы для изучения
1. Методы оценки и снижения рисков инвестиционного портфеля.
2. Метод Марковица в принятии решений.
3. Ковариация и дисперсия (свойства).
4. Матрицы. Обратная и единичная матрицы.
5. Умножение матриц.
6. Дисперсия Портфеля и правило 3-х s (трех “сигм”)