Задача 19.1. Имеются 2 ценные бумаги с доходностями 20 и 5. Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 1.
Задача 19.2. Имеются 2 ценные бумаги с доходностями 30 и 10. Составить портфель ценных бумаг, обеспечивающий доходность 20%. В ответе указать долю в портфеле бумаги номер 1.
Задача 19.3. Имеются 2 ценные бумаги с доходностями 20 и 5. Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 2.
Задача 19.4. Известны доходности пяти ценных бумаг за семь временных периодов.
| Период | R1 | R2 | R3 | R4 | R5 |
Найти по методу Марковица оптимальный состав портфеля, обеспечивающий доходность 10%.
ТЕМА 20. ФОРМИРОВАНИЕ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ ПО МЕТОДУ ШАРПА
Основные теоретические сведения темы
Метод Шарпа появился несколько позже метода Марковица и является логическим развитием этого метода. Развитием является, потому что в ту пору электронных таблиц не было, приходилось численными методами решать системы линейных алгебраических уравнений и старались сделать так, чтобы решить эту систему было бы немножко попроще, полегче, чтобы матрица была по прозрачнее. Чтобы в левой матрице было побольше «0».
Идеи метода Шарпа основаны на определенном наблюдении и на фактах. Факты говорят о следующем: 1.существуют периоды повышенной деловой активности, доходности. 2. Периоды, когда доходность ценных бумаг выше, чем обычно.
Это еще ничего не значит, в среднем доходность выросла, а у каких-то бумаг в этот момент она падает. Для экономики перерабатывающего производства если падает сырье, то растет доходность перерабатывающего производства, но при этом падает доходность добывающей промышленности.
Средняя доходность по рынку. У нас доходность каждой бумаги в отдельности:
r1, r2,r3………rn
(r1, r2,r3………rn) rm – где rm – средняя доходность рынка
В простейшей модели: rm= 
Есть бумаги эмитенты, которые выпущены в большом объеме и находятся у большого количества инвесторов на руках, следовательно, они вносят больший вклад в среднюю доходность. Это называется техникой усреднения.
Доходность каждой бумаги в отдельности - ri связана с – rm и находится в функциональной зависимости от средней доходности каждой отдельной бумаги на рынке ri = f(rm).
Может быть положительной, т.е. чем доходность рынка больше, тем больше ri.
Может быть отрицательной, т.е. на рынке хорошо, а у них идет в убыток.
F(x) =f(x0) +KΔx
Слабо меняющаяся функция.
Примеры решения типовых задач
Пример 20.1. Даны значения
| x | x cp = 3 | |||||
| y | ycp= 29,6 | |||||
| хy | хyср= 109,4 | |||||
(х-хср 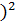
|
Надо построить зависимость.
Для того чтобы построить зависимость нам
Нужен средний Х:
Средний Х = (1+2+3+4+5)/5 = 15//5 = 3
Нужен средний Y:
Средний Y = (7+22+28+43+48) / 5 = 148/5 = 29,6
Также нам понадобиться расчет ковариации:
Ковариация =((7+44+84+172+240)/5) – 3*29,6 = 109,4-88,8 = 20,6
Произведем расчет дисперсии:
Дисперсия = (4+1+0+4+1) / 2 = 5
Коэффициент бета = 20,6 / 2 = 10,3
Коэффициент альфа = 29,6 –(10,3*3) = 29,6 – 30,9 = - 1,3
Корреляция со средним уровнем цен является основополагающей.
Принцип, на котором основам метода Шарпа заключается в том, что доходность каждой бумаги “ri” ri = альфаi + ßirm
При всем при этом данные величины не совсем точные. Величина «ßirm» известна с погрешностью сигма остаточная.
расчет суммарной доходности портфеля:
Суммарная доходность портфеля Rп = ∑wi(альфаi + ßirm) =
W1+W2…..Wn = 1