!Проверь, не делаешь ли ты так!
1.arccos(-0,5) = -  , это неверно. Правильно будет так: arccos(-0,5) = π -
, это неверно. Правильно будет так: arccos(-0,5) = π -  = =
= =  ,
,
т.к. арккосинусом числа -0,5 называется угол, заключенный в промежутке  , косинус которого равен -0,5.
, косинус которого равен -0,5.
2. Решение уравнения cos4x = 0,5, x =  , это неверно, правильно будет: x =
, это неверно, правильно будет: x = 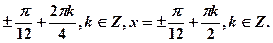
3.При решении уравнения 2sinx +cosx = 1 получают  , это не-
, это не-
верно, уравнение 2sinx +cosx = 1 не однородное относительно sinx и cosx, его решение приведено в п.3.
Контрольный тест
1.Вычислите: аrccos(-1) + arcsin(-1) + arctg(-1).
2.Решите уравнение: а) sin 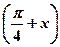 = 0,5; б) tgx = 2; в) cos
= 0,5; б) tgx = 2; в) cos  .
.
3.Решите уравнение:
а) 8sin x + cos2x +7= 0; б) sin2 x +2sinxcosx - 3cos2x +2 = 0;
в) 3sinx - 4cosx = 0.
Свойства обратных тригонометрических функций в таблицах(5)
| Функция Свойства | y= arcsinx | y =arccosx | y=arctgx |
| Область определения (D) | [-1;1] | [-1;1] | (-∞;+∞) |
| Множество значений (E) | [-π/2;π/2] | [0;π] | (-π/2;π/2) |
| Четность или нечетность функции | Нечетная | Не является четной и не является нечетной | Нечетная |
| Знаки функции | аrcsinx <0 для
 ,
аrcsinx >0 для ,
аrcsinx >0 для

| arccosx >0для
 , ,
| arctgx > 0 для

|
| Нули функции | x=0 | x=1 | x=0 |
| Промежутки возрастания | [-1;1] | - | (-∞;+∞) |
| Промежутки убывания | - | [-1;1] | - |
| Наибольшее значение | π/2 | π | - |
| Наименьшее значение | - π/2 | - | |
| Графики | 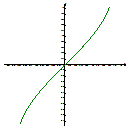
| 
| 
|
Тестовые задания: свойства обратных тригонометрических функций в таблицах (6)
| Задание | Ответы | |
| Значение выражения arcsin (sin360º) равно | 1) 180°; 2) 0°; 3) 90°; 4) 180°; 5) 360°. | |
| Значение выражения arcsin (sin3) равно | 1) π-3; 2)3; 3)π/2-3; 4)3- π /2; 5) 2 π-3 | |
| Значение выражения arccos (cos3) равно | 1) π-3; 2)3; 3)π/2-3; 4)3- π /2; 5) 2 π-3 | |
| Значение выражения arcsin (cos3) равно | 1) π-3; 2)3; 3)π/2-3; 4)3- π /2; 5) 2 π-3 | |
| Значение выражения arcsin(sin4) равно | 1) π-4; 2)4; 3)π/2-4; 4)4- π /2; 5) π-4 | |
| Значение выражения arcsin(sin13) равно | 1) π-13; 2)13; 3)π/2-13; 4)13- 4π; 5) 4 π-13 | |
| Значение выражения arccos (cos10) равно | 1) π-10; 2)10; 3)π/2-10; 4)10- 4π; 5) 4 π-10 | |
| Значение выражения arctg(tg34) равно | 1) 11π-34; 2)34; 3)7π/2-34; 4)34- 11π; 5) 4 π-34 | |
| Решите уравнение arccos(x-2) = π/3 | 1) π/3-+2; 2)2,5; 3)2,5; 4) 1,5; 5) 2π/3 | |
| Решите уравнение arcsin (x2 +2x -2,5) = π/6 | 1) π/6-2,5; 2)2;-1; 3)-3;1; 4) 1;2; 5) π/3; -π/3 | |
| Решите уравнение arctg(tg3x) = - π/4 | 1) -3; 2)-1/4; 3)-π/12; 4)3- π /4; 5) -4 π | |
| Упростите выражение аrctg2,4- arccos0,6 | 1) аrctg 16/63; 2)1,8; 3)-16/63; 4)3; 5) -0,2 | |
Найдите область определения функции 
| 1) [-1;1]; 2) [1;3) 3) (1;3); 4) (-1,1); 5) [1;3] | |
| Решите неравенство arcsinx < 2arccosx | 1) [-1;1/2]; 2) [1/2;3)
3) (-1;1); 4)  5)
5) 
| |
Решите неравенство 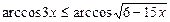
| 1)1; 2)(1/3;2,5) 3)-1/3; 4) (-1;1); 5) 1/3 | |
Решите уравнение 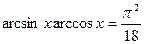
| 1)1; 2)-1/2;1.
3)-1/3;1 4)-1;1; 5) 
| |
Решите уравнение 
| 1)1/2; 2)-1/2;1.
3)-1/3;1 4)-1;1; 5) 
| |
Решите уравнение 
| 1)1; 2)2. 3)-1; 4)-1;1; 5)-2 | |
Решите уравнение 
| 1)1; 2)2. 3)-1; 4)-1;1; 5) -0,5 | |
| Решите неравенство arccosx >arccos(3x-1) | 1) [-1;1/2]; 2) [1/2;3)
3) (-1;1); 4)  5) (1/2;2/3]
5) (1/2;2/3]
| |
Решите уравнение
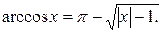
| 1) -1;
2)-1/2;1.
3)-1/3;1
4)-1;1; 5) 
| |
Решите уравнение

| 1.  2)(-1;1); (-π;π).
3)(-1;1)
4) (-π;π);(-1;1); 5)
2)(-1;1); (-π;π).
3)(-1;1)
4) (-π;π);(-1;1); 5) 
| |
Решите уравнение

| 1.0,5.2)0. 3)-1; 4)-1;5)π/2 | |
Наибольшее значение функции  равно равно
| 1)1; 2)0. 3)-1; 4)-1;5)π/2 | |
Наибольшее значение функции 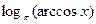 равно равно
| 1)1; 2)0. 3)-1; 4)-1;5)π |
Виды тригонометрических уравнений в таблицах(7)
| Тип уравнения | Метод решения | Применение | Примечания |
| Простейшие тригонометрические | sinx = a
a>1 или a< -1,не имеет решений.
a= 1, x=  a= -1,
x= -
a= -1,
x= -  a= 0, x=
a= 0, x= 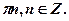 a|
a| 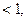 x= (-1)narcsina + πn, n
x= (-1)narcsina + πn, n  . .
| При решении тригонометрических уравнений, сводящихся к простейшим, используется общий вид решения | При отыскании решений, принадлежащих некоторому отрезку, можно не использовать общий вид решения уравнения. |
cosx =a
a>1 или a< -1 не имеет решений.
a = 1 решение уравнения: x=  a= -1, то x=
a= -1, то x=  a= 0, x=
a= 0, x=   -1≤a
-1≤a  то x= то x=  arccosa+2πn, n arccosa+2πn, n  . .
| При решении тригонометрических уравнений, сводящихся к простейшим, используется общий вид решения | ||
tgx = a
x=arctga + πn, n  . .
| При решении тригонометрических уравнений, сводящихся к простейшим, используется общий вид решения | ||
| Уравнения, в которых можно выполнить замену переменной | af2(x) + b f(x)+c= 0, где f(x) – некоторая тригонометрическая функция | Уравнение относительно f(x) может быть более высокой степени, чем вторая. | Функция f(x) – может быть представлена выражением, содержащим тригонометрические функции. |
| Однородные тригонометрические уравнения. | a∙sin2x+bsinxcosx+ k∙cos2x= 0, a,b,k – некоторые числа. Если a≠0, k≠0, то уравнение a∙sin2x+bsinxcosx+ k∙cos2x= 0 равносильно уравнению atg 2x +btgx +k =0, т.е. обе части уравнения делятся на cos2x | Однородное уравнение относительно sinx и cosx может быть первой степени или более высокой степени, чем вторая. | Если уравнение – неполное однородное, то деление на функцию в степени однородности может привести к потере корней. |
| Уравнение вида asinx+bcosx=c | Привести к виду sin(x +t) = 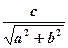 t = arctg b/a
t = arctg b/a
| Применяется в случае, если с≠ 0. Следует привести к виду, когда a >0 | Частные случаи

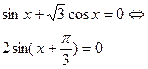
|
| Уравнения, решаемые с помощью разложения на множители левой части уравнения | Использовать условие равенства произведения нескольких множителей нулю | Если в правой части уравнения – ноль, а в левой – произведение тригонометрических функций, то на общей области определения функций уравнение равносильно совокупности уравнений: каждый множитель равен нулю | Полученные решения совокупности уравнений могут содержать общие корни. |
| Уравнения, решаемые с помощью применения свойства ограниченности тригонометрических функций |
 ,
f(x) ,
f(x) 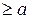 , g(x) , g(x)  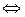 
| Применяется к сумме af(x)+ bg(x)= a+b, где f(x) и g(x) одна из тригонометрических функций sinkx или costx | В уравнении
 ,
g(x) может быть любой функцией.
Например, ,
g(x) может быть любой функцией.
Например, 
|
Уравнение содержит
только выражение  ( ( )
и функцию )
и функцию 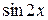 или или

| Решается с помощью замены:
 , ,  (
(  ) )
| Замена применяется в случае, когда коэффициенты перед sinx и cosx – имеют равные модули. |
   Сделаем замену Сделаем замену  . Тогда: . Тогда:
 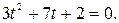   
 Нет кор Нет кор    . .
|
Тестовые задания: основные типы тригонометрических уранений(8)
| Задание | Ответы | |
Решите уравнение

| 1.  2.Ø
3. 2.Ø
3.  4.
4.  5.
5. 
| |
Решите уравнениe

| 1.  2.Ø
3. 2.Ø
3.  4.
4.  5.
5. 
| |
Решите уравнение

| 1.  2.Ø
3. 2.Ø
3.  4.
4.  5.
5. 
| |
Решите уравнение

| 1.  2.Ø
3. 2.Ø
3.  4.
4.  5.
5. 
| |
Решите уравнение

| 1.  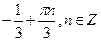 2.Ø
3.
2.Ø
3.  4.
4.  5.
5. 

| |
Решите уравнение

| 1.Ø
2.  3.
3.  4.
4.  5.
5. 
| |
Решите уравнение

| 1.  2.
2.  3.
3.  4.
4.  5.
5. 
| |
Решите уравнение
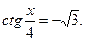
| 1.  2.
2.  3.
3.  4.
4.  5.
5. 
| |
Решите уравнение

| 1.  2.
2.  3.
3.  4.
4.  5.
5. 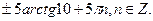
| |
Решите уравнение

| 1.  2.
2.  3.
3. 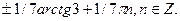 4.
4.  5.
5. 
| |
Решите уравнение

| 1.  2.
2.  3.
3. 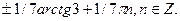 4.
4.  5.
5. 
| |
Решите уравнение
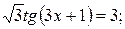
| 1.  3.
3.  4.
4. 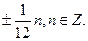 5.
5. 
| |
Найдите все корни уравнения  , принадлежащие промежутку
(-1;1) , принадлежащие промежутку
(-1;1) 
| 1.  2.
2.  3.
3.  .
4. .
4. 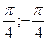 .
5.. .
5.. 
| |
Решите уравнение:

| 1. 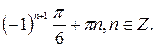 2.
2. 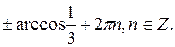 3.
3. 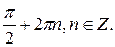 4.
4. 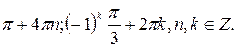 5
5 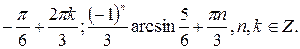
| |
Решите уравнение:

|
1. 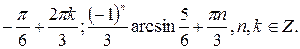 2.
2. 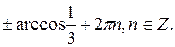 3.
3. 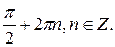 4.
4.  5..-
5..- 
| |
Решите уравнение:

| 1. 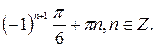 2.
2. 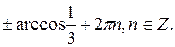 3.
3. 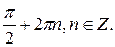 4.
4. 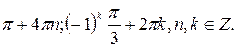 5.-
5.- 
| |
Решите уравнение:
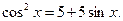
| 1.-  2.
2.  3.
3.  4. p/2 + pn, nÎZ;
5.
4. p/2 + pn, nÎZ;
5. 
| |


| 1.  2.
2.  3.
3.  4. p/2 + pn, nÎZ;
5.
4. p/2 + pn, nÎZ;
5. 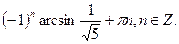
| |

| 1.  2.
2.  3.
3.  4. p/2 + pn, nÎZ;
5.
4. p/2 + pn, nÎZ;
5. 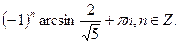
| |

| 1.  2.
2.  3.
3.  4. p/2 + pn, nÎZ;
5.
4. p/2 + pn, nÎZ;
5. 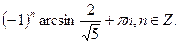
| |

| 1.  2.
2.  3.
3.  4. p/3 + pn, nÎZ;
5.
4. p/3 + pn, nÎZ;
5. 
| |
 . .
| 1. 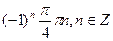 2.
2.  3.
3.  4. p/3 + pn, nÎZ;
5.
4. p/3 + pn, nÎZ;
5. 
| |

| 1. 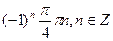 2.
2.  3.
3.  4. p/3 + pn, nÎZ;
5.
4. p/3 + pn, nÎZ;
5. 
| |

| 1. Ø
2. 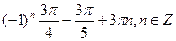 3.
3.  4.
4.  5. p/3 + pn, nÎZ;
5. p/3 + pn, nÎZ;
| |
Решите уравнение: 
| 1.  2.
2. 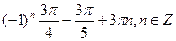 3.
3.  4.
4.  5. p/3 + pn, nÎZ;
5. p/3 + pn, nÎZ;
| |
| Решите уравнение: sinx - 2cosx = 0 |
1.  2.
2.  3.arctg 2 + pn, nÎZ.
4.
3.arctg 2 + pn, nÎZ.
4.  5. p/3 + pn, nÎZ;
5. p/3 + pn, nÎZ;
| |
Решите уравнение: 
| 1.  2.
2. 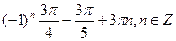 3.
3.  4.
4.  ,p/3 + pn, nÎZ;
5.2pn, nÎZ; p/2+2pn, nÎZ ,p/3 + pn, nÎZ;
5.2pn, nÎZ; p/2+2pn, nÎZ
| |
| Решите уравнение: 1 + 7 cos 2 x = 3 sin 2x | 1.arctg4 + 2  k,
arctg2 + 2 k,
arctg2 + 2  k, k k, k  2. 2.
2. 2. 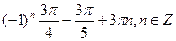 3.
3. 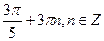 ; ;  4.
4.   5. p/3 + pn, nÎZ;
5. p/3 + pn, nÎZ;
|
Тестовые задания: различные тригонометрические уравнения (9)
| № | Задание | Ответы |
| 1. | Решите уравнение: 
| 1.  2.
2. 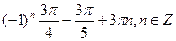 3.
3.  4.
4.  5. p/3 + pn, nÎZ;
5. p/3 + pn, nÎZ;
|
| 2. | Решите уравнение: tgx – 2ctgx + 1 = 0 | 1. 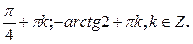 2. pn, nÎZ;
3. p+ pn, nÎZ;
4. p
5. p/2 + pn, nÎZ;
2. pn, nÎZ;
3. p+ pn, nÎZ;
4. p
5. p/2 + pn, nÎZ;
|
| 3. | Решите уравнение: cos 2x = 1 + 4 cosx | 1. 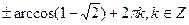 2..
2..  3.
3.  4.
4. 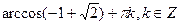 5. p/4 + pn, nÎZ;
5. p/4 + pn, nÎZ;
|
| 4. | Решите уравнение:  = = 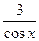
| 1.2pn, nÎZ;
2. pn, nÎZ;
3. p+ pn, nÎZ;
4.  5. p/2 + pn, nÎZ;
5. p/2 + pn, nÎZ;
|
| 5. | Решите уравнение 
| 1. (π+2pn;3/2p +2pn), nÎZ; 2. pn, nÎZ; 3. p+ pn, nÎZ; 4. (-π+2pn;0+2pn), nÎZ; 5. p/2 + pn, nÎZ; |
| 6. | Решите уравнение

| 1.  .
2. .
2. 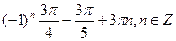 3.
3.  4.
4. 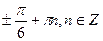 5.
5. 
|
Решите уравнение: 
| 1.-p/24+pn/2,nÎZ
p/12+pk,kÎZ.
2. 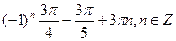 3.
3.  4.
4.  5.
5. 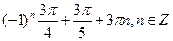
| |
Решите уравнение 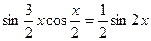
| 1.p/2+2pn, nÎZ 2. pn, nÎZ; 3. p+ pn, nÎZ; 4. (p/2)n, nÎZ; 5. p/2 + pn, nÎZ; | |
Решите уравнение: 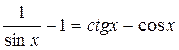
| 1.p/2+2pn, nÎZ 2. pn, nÎZ; 3. p+ pn, nÎZ; 4. (p/2)n, nÎZ; 5. p/2 + pn, nÎZ; | |
Решите уравнение: 
| 1.pn, nÎZ; ±3p/4+2pn, nÎZ. 2.-p/24+pn/2,nÎZ p/12+pk,kÎZ 3. p+ pn, nÎZ; 4. (p/2)n, nÎZ; 5. p/2 + pn, nÎZ; | |
Решить уравнение: 
| 1. -p/4+pn, nÎZ. 2.-p/2+pn/2,nÎZ 3. p+ pn, nÎZ; 4.p+4pn, nÎZ. 5. p/2 + pn, nÎZ; | |
| Решить уравнение: 5sin2x-sin6x+6=0 | 1.-p/4+pn, nÎZ. 2.-p/2+pn/2,nÎZ 3. p+ pn, nÎZ; 4.p+4pn, nÎZ. 5. p/2 + pn, nÎZ; | |
Найдите корни уравнения 
| 1.  2.
2.  3.
3.  4.
4.  .
5. .
5.  . .
| |
| 14. | Найти корни уравнения (sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку [0; 2p]. | 1.  2. p;
3. 2p; p;
4.0;
5. p/2; p
2. p;
3. 2p; p;
4.0;
5. p/2; p
|
| Решите уравнение: sin2x – sinx = 2cosx – 1 | 1.   2
2  3.
3.  4.
4.  .
5. .
5.  . .
| |
Решите уравнение: 
| 1.  2. 1;p;
3. 2p; p;
4.0;1/
5.
2. 1;p;
3. 2p; p;
4.0;1/
5.  . .
| |
Решите уравнение: 
| 1.  . 2 . 2  3.
3.  4.
4.  .
5. .
5.  . .
| |
Решите уравнение: 
| 1.  2.-5/12.
3.
2.-5/12.
3.  4.
4.  .
5. .
5.   ,
-5/12. ,
-5/12.
| |
Решите уравнение: 
| 1.  .
2.-p/2+pn/2,nÎZ
3. p+ pn, nÎZ;
4.p+4pn, nÎZ.
5. p/2 + pn, nÎZ; .
2.-p/2+pn/2,nÎZ
3. p+ pn, nÎZ;
4.p+4pn, nÎZ.
5. p/2 + pn, nÎZ;
| |
Наименьший целый корень уравнения  равен равен
| 1.2; 2.5; 3.0; 4.-5 5. 6 | |
Число корней уравнения  равно равно
| 1.2; 2.5; 3.4; 4.3 5. 6 | |
Наибольший целый корень уравнения 
| 1.10; 2.12; 3.4; 4.5 5. 6 | |
Решите уравнение: 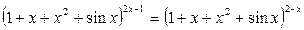
| 1.0; 1. 2.0;-1. 3.0;1; p+ pn, nÎZ; 4.1;p+4pn, nÎZ. 5. 0; p/2 + pn, nÎZ; | |
| Решите уравнение: sin x sin 5x = 1 | 1.  2.-p/2+pn/2,nÎZ
3. p+ pn, nÎZ;
4.p+4pn, nÎZ.
5. p/4 + pn, nÎZ;
2.-p/2+pn/2,nÎZ
3. p+ pn, nÎZ;
4.p+4pn, nÎZ.
5. p/4 + pn, nÎZ;
| |
| Решите уравнение: sin1000 x+cos500x=1 |
1.-p/2+pn/2,nÎZ
2. 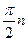 , nÎZ.
3. p+ pn, nÎZ;
4.p+4pn, nÎZ.
5. p/2 + pn, nÎZ; , nÎZ.
3. p+ pn, nÎZ;
4.p+4pn, nÎZ.
5. p/2 + pn, nÎZ;
| |
| Решите уравнение: tg4x + tg4y + 2ctg2x ctg2y = 3 + sin2(x+y) | 1. (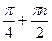 ; ; 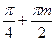 );
m + n = 2k.
2. );
m + n = 2k.
2. 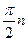 , , 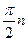 ,nÎZ.
3. p+ pn, nÎZ;
4.p+4pn, nÎZ.
5. p/2 + pn, nÎZ; ,nÎZ.
3. p+ pn, nÎZ;
4.p+4pn, nÎZ.
5. p/2 + pn, nÎZ;
| |
| Решите уравнение:x2 +4x cos y +4 =0 | 1.(-2; 2pn) nÎZ; (2;p+ 2pn), nÎZ; 2) (-2;pn),(2; p+p) 3. (2;p+ pn), nÎZ; 4. (0,25;p+4pn), nÎZ. 5. (-1;p/2 + pn), nÎZ; | |
| Решите уравнение: sinx=x2+x+1 | 1)  n, nÎZ; 2) Æ; 3) 4)- n, nÎZ; 2) Æ; 3) 4)-  ;
5) ;
5)  . .
| |
Решите уравнениеsinx+cosx= 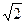 +sin4x и в ответ запишите сумму корней уравнения Î [-2p: 2p] +sin4x и в ответ запишите сумму корней уравнения Î [-2p: 2p]
| 1)  ; 2) - ; 2) -  ; 3) ; 3)  . 4) 2;
5) -2; . 4) 2;
5) -2;
| |
| Решите уравнение: x2 -4x cos y +4 =0 | 1.(-2; 2pn) nÎZ; (2;p+ 2pn), nÎZ; 2. (-2;pn),(2; p+pn), nÎZ.. 3. (-2; 2pn) nÎZ; (2;p+ 2pn), nÎZ; 4. (0,25;p+4pn), nÎZ. 5.(2;2pn),(-2; p+2pn), nÎZ.. | |
| Решите уравнение: 4sin x – 21+sin x cos xy +2│y│=0 | 1.(πn;0) nÎZ; 2 (-2;pn),(2; p+pn), nÎZ.. 3. (-2; 2pn) nÎZ; (2;p+ 2pn), nÎZ; 4. (0,25;p+4pn), nÎZ. 5.(2;2pn),(-2; p+2pn), nÎZ.. | |
Решите уравнение:
│1+ cos (p  )│+│x2 - 15x + 44 │= 15x- x2 - cos (p )│+│x2 - 15x + 44 │= 15x- x2 - cos (p  ) - 45 ) - 45
| 1.9; 2.π; 3.4π; 4.5π; 5. 6. | |
Решите уравнение:

| 1. 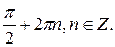 2) Æ; 3).
2) Æ; 3).  4)- 4)-  ;
5) ;
5) 
| |
Решите неравенство 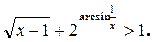
| 1.[1; +∞).
2. ½
3.  4.
4.  5.1.
5.1.
| |
Сколько корней имеет уравнение  ? ?
| 1.7; 2.8; 3.3; 4.9; 5.1 | |
Решите уравнение: 
| 1.[1; +∞).
2. ½
3.  4.
4.  5.1.
5.1.
| |
Решить неравенство:
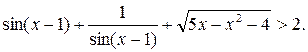
| 1.[1; +∞).
2.(½;4)
3.  4.(1;4].
5.(1;4)
4.(1;4].
5.(1;4)
| |
| Решите уравнение: tg (5x + 1) + tg (x-6) = 0. | 1)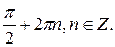 2) Æ; 3).
2) Æ; 3).  4)-
4)-  ;
5) ;
5)  , где р , где р 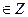
| |
Решите уравнение: 
| 1)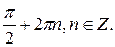 2) Æ; 3).
2) Æ; 3).  4)
4)  -
5) -
5)  , где р , где р 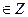 4. 4.
| |
Решите уравнение: 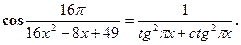
| 1.x= 0,25.
2.  3.
3.  4.
4. 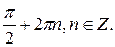 5.1
5.1
| |
Решите уравнение: 
| 1)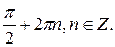 2) Æ; 3).
2) Æ; 3).  4)-
4)-  ;
5) ;
5)  , где р , где р
| |
| Решите уравнение: 2cos πx=2x-1 | 1.  2.
2.  3.
3. 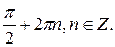 4.0,5;
5.-1.
4.0,5;
5.-1.
| |
Решите уравнение:

| 1.  2.
2.  3.
3. 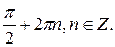 4.0,5+πk;
5.-1.
4.0,5+πk;
5.-1.
| |
Решите уравнение: 
| 1.  2.
2.  3.
3. 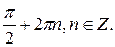 4.0,5+πk;
5.-π.
4.0,5+πk;
5.-π.
| |
Решите уравнение: 
| 1.  2.
2.  3.
3. 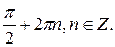 4.0,5+πk;
5.-π..
4.0,5+πk;
5.-π..
| |
| Решите уравнение: cosx=x2 +2x+2 | 1)-1;
2) Æ;
3)  4)
4)  ;
5)0. ;
5)0.
| |

| 1.  2) Æ;
3)
2) Æ;
3)  4)
4)  ;
5) ;
5)  . .
|
Тема 4* Производная
Проверочный тест:
1.Найдите производную функции а) f(x) = 2x +5; б) f(x) = (3x -7)(4x+9);
в)f(x) =  , г) f(x) =3x5.
, г) f(x) =3x5.
2.Найдите f '(2), если а) f(x) = 8x +5; б) f(x) = (3x -7)(4x+9);
в)f(x) =  ; г) f(x) =3x5.
; г) f(x) =3x5.
3.Найдите f '(x), если а) f(x) =  ; б) f(x) =
; б) f(x) =  ;
;
в)f(x) = (1-3x)4; г) f(x) =  .
.
4.Найдите f '(x), если а) f(x) = sinx;б) f(x) = cos2x;
в)f(x) = tg3x; г) f(x) = ctg  .
.
Ответы:
1. a) 2; б)24x-1; в)  ; г)15x4.
; г)15x4.
2. a) 8; б) 47; в)  ; г) 240.
; г) 240.
3. a)  ; б)
; б)  ; в) -12(1-3x)3; г)
; в) -12(1-3x)3; г)  .
.
4. a) cosx; б) -2sin2x; в)  ; г)
; г) 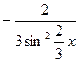 .
.
Улучшите свои знания
1.Производная суммы, произведения, частного, степени.
а)производная суммы двух функций (U и V) вычисляется по формуле
(U + V)' = U' + V',
в предположении, что производные слагаемых(U' и V') существуют.
Иначе: производная суммы двух дифференцируемых функций равна сумме производных этих функций.
Замечания
1.1 Производная постоянной равна нулю: с'=0.
1.2 Производная от x равна 1: (x'=1).
1.3 Производная от kx+b равна k: (kx+b) ' = k.
1.4 Постоянный множитель можно выносить за занак производной,
например, (2x)'=2(x)'=2
Пример, (2x+5)' = (2x) '+ 5' = 2+0 =2.
б)производная поизведения двух функций (U и V) вычисляется по формуле
(U ∙ V)' = U'V + V'U,
в предположении, что производные множителей (U' и V') существуют.
Например, ((3x -7)(4x+9)) ' = (3x-7)'(4x+9) +(3x-7)(4x+9)' =3(4x+9)+4(3x-7) =
12x+27 +12x-28 = 24x -1.