!Проверь, не делаешь ли ты так!
1. Найдите промежутки монотонности функции f(x) =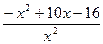 
;
Ответ: функция возрастает на промежутках (- ∞; 0) и (3,2; +∞),
функция убывает на промежутке (0; 3,2).
Этот ответ неверный, ошибка в решении неравенств f' (x)>0 и f' (x)< 0.
f' (x) =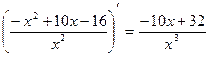 
;
Решением неравенства f' (x)>0 будет промежуток (0; 3,2);
решением неравенства f' (x)< 0, будут промежутки (- ∞; 0) и (3,2; +∞)
Правильный ответ: функция убывает на промежутках (- ∞; 0) и [3,2; +∞),
функция возрастает на промежутке (0; 3,2], так в точке x=3,2 данная функция непрерывна, а x=0 точка разрыва.
2. Найдите наибольшее и наименьшее значение функции f(x) = 2x3-6x на отрезке [0; 1,5].
Ответ: наибольшее значение функции на этом отрезке равно 4.Этот ответ неверный, ошибка в том, что критическая точка -1 не принадлежит отрезку [0; 1,5].
Правильный ответ: наибольшее значение функции на этом отрезке равно 0; наименьшее значение функции на этом отрезке равно -4.
Контрольный тест
1. Найдите промежутки монотонности и точки экстремума функции
у =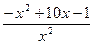 
;
2. Исследуйте функцию и постройте ее график у= 0, 5x4 +8x.
3. Найдите наибольшее и наименьшее значение функции f(x) = x3-3x
на отрезке [0; 1,5].
4. Составьте уравнения касательных, проведенных к графику функции
y = x2- 1 в точках ее пересечения с осью Ox.
Тема 7 Корень n-ой степени из числа
Проверочный тест:
1.Верно ли, что а) 
б) 
в)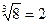 
?
2.Решите уравнение: а) x4 =0,0016; б) x6 = 64; в) x5 =32.
3.Упростите выражение: а) 
б) 
в) 
г) 
;
д) 
4.Решите уравнение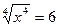 
.
5.Упростите выражение: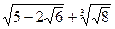 
.
Ответы:
1.а)верно; б) неверно; в)верно. 2. а)0,2; -0,2; б)2;-2; в)2.
3..а)5; б)3; в)0,25; г)8;д)2. 4. 6; -6; 5. 
Улучшите свои знания
1.Арифметическим корнем n- ой степени из числа a называетсянеотрицательное число, n- ая степень которого равна a.
Обозначается 
.
Например,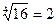 
- это равенство верно, так как 24 =16, 2>0, но
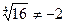, так как – 2<0.
Корнем n- ой степени из числа a называется число, n- ая степень которого равна a.
Например, корень четвертой степени из числа 16 – это число 2, а также и число -2, так как 24 =16 и (-2)4 =16. Корень пятой степени из числа 32 только один, он равен 2, так как 25=32.
а) Решить уравнение x4 =15.
По определению корня четвертой степени число x – корень четвертой степени из числа 15.
Таких корней два - арифметический и ему противоположный 
Ответ: 
б) Решить уравнение x6 =0, 000001.
По определению корня шестой степени число x – корень шестой степени из числа 0, 000001.
Таких корней два - арифметический и ему противоположный 
или 0,1 и -0,1.
Ответ: 0,1 и -0,1.
в) Решить уравнение x5 =243.
По определению корня пятой степени число x – корень пятой степени из числа 243, т. е. 3.
Ответ: 3.
Свойства корней n- ой степни
Для любых натуральных m и к, целого n и любых неотрицательных чисел a и b выполняются равенства:
а) 
, к>0, например, 
.
б) 
например, 
в) 
например, 
.
г) 
например,) = 
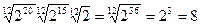
д)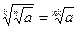 
, например, 
.
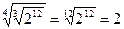Основные тождества
а)Для любого действительного числа a и для n – четного верно равенство:
.
б)Для любого действительного числа a и для n – нечетного верно равенство:
.
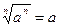Например,
в)Для любого неотрицательного числа a и n –натурального верно равенство:
.
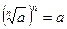Например,
разложить на множители x - 4, где x >0.
Представим x в виде 
, тогда получим x- 4= -4 =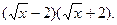 
Примеры
1. Решите уравнение: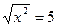 
.
Решение: по основному тождеству 4а)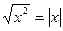 
, значит, данное уравнение заменим на равносильное │x│=5, откуда x=5 или x =-5.
Ответ: 5, -5.
2.Упростите выражение .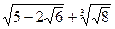
Решение: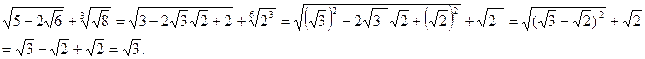 
3. Упростите выражение 
.
Решение
1.Умножим числитель и знаменатель каждой дроби на сопряженное выражение знаменателю, получим:
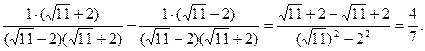
4.Упростите выражение:
= 
.
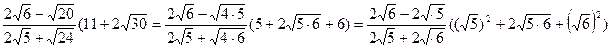
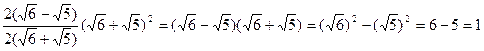2. Сравните числа:
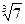и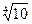 
.
Решение:
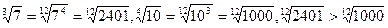, значит > .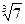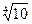