а) Если a>1, то неравенство af(x)> ag(x) равносильно неравенству
f(x)> g(x),(неравенство af(x)< ag(x) равносильно неравенству f(x)< g(x))
Например, неравенство 33x-2 >36-x равносильно неравенству 3x-2>6-x, решая это неравенство(4x>8, x>2), получим x  .
.
б) Если 0< a<1, то неравенство af(x)> ag(x) равносильно неравенству
f(x< g(x),(неравенство af(x)< ag(x) равносильно неравенству f(x)> g(x))
Например, неравенство 0,33x-4 <0,36- 2x равносильно неравенству
3x-4>6-2x, решая это неравенство(5x>10, x>2), получим x  .
.
Наиболее часто встречающиеся ошибки:
!Проверь, не делаешь ли ты так!
1. 0,1x >0,12 (1), x>2 (2). Из неравенства ( 1 ) не следует неравенство (2).
Правильно будет: 0,1x >0,12 , x<2.
2.Решить неравенство: 9x -8∙3x - 9 >0.
(⅓)2x -8∙(⅓) x -9>0, пусть (1/3)x =y, тогда данное неравенство будет иметь вид:
y2 -8y – 9>0.
Найдем корни уравнения y2 -8y – 9=0, получим: y=9 или
y=-1.Cледовательно, (1/3)x =9 или (1/3)x =-1. Уравнение (1/3)x =9 имеет один корень, равный -2, уравнение (1/3)x =-1 не имеет решений, учитывая знак неравенства, получим ответ x>-2. Это решение неверно.
Правильное решение:
y2 -8y – 9>0 решим это неравенство методом итервалов, получим y>9
или y <-1. Возвращаясь к замене, получим (1/3)x >9 или(1/3)x <-1.
Решение первого неравенства: x< -2, x  (-∞;-2)(основание показательной функции 1/3 <1), второе неравенство решений не имеет.
(-∞;-2)(основание показательной функции 1/3 <1), второе неравенство решений не имеет.
Ответ: (-∞;-2).
Контрольный тест
1.Решить уравнение:
а)  ; б) (0,5)x =
; б) (0,5)x = 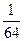 ; в) 2x+1 +2x =6;
; в) 2x+1 +2x =6;
2. Решите неравенство:
а)  ; б) (0,5)x <
; б) (0,5)x < 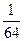 ; в) 2x+1 +2x >6;
; в) 2x+1 +2x >6;
3. Решите уравнение:
а)52x -6∙5x +5=0; б) 0,22x +0,2x -2 =0.
4. Решите неравенство:
а)52x -6∙5x +5<0; б) 0,22x +0,2x -2 <0.
Свойства показательной функции в таблице (20)
| Свойства функция | y = a x , a >1 | y = ax, 0 <a < 1 |
| Область определения (D) | D(a x ) =(- ∞;+ ∞) | D(lоga x) =(- ∞;+ ∞) |
| Множество значений (E) | E(lоga x) =(0;+ ∞) | E(lоga x) =(0;+ ∞) |
| Нули функции | a x =0, x  Ø Ø
| a x =0, x  Ø Ø
|
| Знаки функции |
a x >0, x  (- ∞;+ ∞) (- ∞;+ ∞)
| a x >0, x  (- ∞;+ ∞) (- ∞;+ ∞)
|
| Промежутки возрастания | y = a x , при a>1 возрастает на всей областиопределения. | |
| Промежутки убывания | y = a x , при 0<a<1убывает на всей области определения. | |
| Графики | 
| 
|
Тестовые задания: применение свойств показательной функции(21)
| № | Задание | Ответ |
| Не меньше, чем 1 являются значения выражений: a) 2-3; b) (½)-1/2 ; c)(½) |x|; d) 10arccosx; e)(1/3)lg(sinx); f)3 -π | 1.c) d); e); f) 2.b);c);d) e) | |
Верным является неравенство:
a) 2-3 >(½)-1/2 ; b) (10+|x|)-1/2 <1; c)(2) |x|+1 ≥2;
d) 10arccosx ≥x ; e)  (1/3)lg(sinx); f)3 –π < x2 -2x +3 (1/3)lg(sinx); f)3 –π < x2 -2x +3
| 1.c) d); e); f) 2.b);c);d);e) f) | |
| Функция f(x) является возрастающей на всей области определения, если a) f(x)=2-x+2; b) f(x)= (½)-1/x ; c) f(x)= (½) |x|; d) f(x)= 10arccosx; e) f(x)= (1/3)sinx; f) f(x)=3arcsinx | 1.c) d); 2.b);c);d);e); f). 3. f). 4.b); | |
Функция f(x) является убывающей на всей области определения, если
a) f(x)=2x -8; b) f(x)= (½)-x ; c) f(x)= (4) -|x|;
d) f(x)= 10arccosx; e) f(x)=  ;
f) f(x)=-3arcsinx ;
f) f(x)=-3arcsinx
| 1.c) d); 2. d);e); f). 3. f). 4.b); | |
Функция f(x) является возрастающей на всей области определения, если
a) f(x)=0,25x -35; b) f(x)= 4(0,25)7-x ;
c) f(x)= 3 1,5x-4 44x+1;
d) f(x)= 102x-5 + x; e) f(x)=  ;
f) f(x)=6x +4x. ;
f) f(x)=6x +4x.
| 1.c) d); 2.b);c);d); f). 3. f). 4.b); 5. b);c);d);e); f). | |
Функция f(x) является убывающей на всей области определения, если
a) f(x)=0,25x -3x; b) f(x)= -4(5)-x ;
c) f(x)= 2 x-4 4-x+1;
d) f(x)= (½)2x-5 - x; e) f(x)=  ;
f) f(x)= 46x +4-4x. ;
f) f(x)= 46x +4-4x.
| 1.c) d); 2.b);c);d); f). 3. f). 4.b); 5.a);d);e). | |
Не меньше 2- х является значение выражений:
a) 2-3 + 2 3; b) (½)-1/2 - (½)1/2 ; c) 5 |x| + 5 -|x| ; d) 102x + 2
e)(1/3)lg(sinx) + 3; f)  + + 
| 1.c) d); 2.b);c);d); f). 3. f). 4.b); 5.a);с); d);e);f). | |
| Наибольшее значение функции y=2sinx равно | 1.0; 2.1; 3. не существует; 4.2; 5. ½. | |
| Наименьшее значение функции y=2 arccosx | 1.0; 2.1; 3. не существует; 4.2; 5. ½. | |
| Множество значений функции y=(1/3) cosx | 1.(0;+∞;) 2.(1;3] 3. [1/3;3] 4.[-1;1]; 5. [-3;3] | |
| Множество значений функции y=(1/3) |x| | 1.(0;+∞;) 2.(0;1] 3. (0;3] 4.[0;1]; 5. [0;1/3] | |
Множество значений функции 
| 1.(1;+∞); 2.(0;1] 3. (0;2] 4.[0;4]; 5. [2; +∞). | |
Множество значений функции 
| 1.(4;+∞);
2.(0;1/4]  [4;+∞)
3.(-∞;1/4] [4;+∞)
3.(-∞;1/4]  [4;+∞)
4.[0;4];
5. [4; +∞). [4;+∞)
4.[0;4];
5. [4; +∞).
| |
 14 14
| Наименьшее значение функции | |
 равно равно
| 1.0;
2.1;
3. не существует;
4. 2;
5. 
| |
Множество значений функции 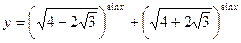
| 1.(2;+∞);
2.(0;1/4]  [4;+∞)
3.(-∞;1/4] [4;+∞)
3.(-∞;1/4]  [4;+∞)
4.[0;4];
5. [4;+∞)
4.[0;4];
5. 
| |
Множество значений функции 
| 1.(4;+∞);
2.(0;1/4]  [4;+∞)
3.(-∞;1/4]
4.[2;4];
5. [4;+∞)
3.(-∞;1/4]
4.[2;4];
5. 
| |
Множество значений функции 
| 1.(4;+∞);
2.(0;2]
3.(-∞;1/4]
4.[1/32;1/2];
5. 
| |
Множество значений функции 
| 1.(10;+∞);
2.(0;1/10]  [10;+∞)
3. (-∞;1/10]
4.[10;100000];
5. [10;+∞)
3. (-∞;1/10]
4.[10;100000];
5. 
| |
Функция y=  является является
| 1.Возрастающей для всех x; 2. Убывающей для всех x; 3. Возрастающей для всех x≥0; 4.Убывающей для всех x≥0; 5. Убывающей для всех x ≠0. | |
Функция
y=  является является
| 1.возрастающей для всех x; 2. убывающей для всех x; 3. возрастающей только для всех x≥0; 4.убывающей только для всех x≥0; 5. убывающей для всех x ≠0. | |
Наибольшее целое отрицательное решение неравенства:

| 1) -2; 2) -5; 3) -1;4) -2; 5) другой ответ |
Решние показательных уравнений и неравенств в таблицах(22)
| № | Вид уравнения, неравенства | Метод решения | Применение | Примечание |
| af(x)=ag(x), где а>0, а≠1 |
af(x)=ag(x) 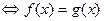 , где а>0, а≠1 , где а>0, а≠1
| Применяется для любого положительного основания, отличного от 1. Если основание содержит переменную величину, то следует отдельно рассмотреть случай, когда основание равно 1, нулю, а так же отрицательно |  .
При условии x > 0, x ≠1, имеем .
При условии x > 0, x ≠1, имеем  0, откуда x =3.По определению степени сцелым показателем основание степени может быть равным 1 и отрицательному числу. Проверяем 1, получаем 11-4 = 1, т.е. 1 – корень уравнения. Среди отрицательных чисел только -1 в четной степени равняется 1. Поэтому возможный отрицательный корень -1.
Проверим: получим (-1)-1-3 = 1, значит x = -1 – корень уравнения. 0, откуда x =3.По определению степени сцелым показателем основание степени может быть равным 1 и отрицательному числу. Проверяем 1, получаем 11-4 = 1, т.е. 1 – корень уравнения. Среди отрицательных чисел только -1 в четной степени равняется 1. Поэтому возможный отрицательный корень -1.
Проверим: получим (-1)-1-3 = 1, значит x = -1 – корень уравнения.
| |
| af(x) = b где а>0, а≠1 | Если b > то уравнение af(x) = b где а>0, а≠1 равносильно уравнению f(x) = loga b | Если основание содержит переменную величину, то следует отдельно рассмотреть случай, когда основание равно 1, нулю, а так же отрицательно. |
 

| |
| Aa2x+Bax+C=0, A≠0. | С помощью подстановки y=ax сводится к квадратному уравнению Ay2+By+C=0. | Применяется для уравнений, содержащих степени af(x) и a 2f(x) или af(x) и a-f(x) . | Подстановка может быть применена к уравнению 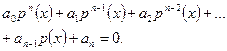 p(x)= af(x) p(x)= af(x)
| |
| Aa2x + Bax bx +Cb2x = 0, A≠0 | Однородное уравнение второй степени. Все члены левой части уравнения разделить на b2x | Применяется для уравнений, содержащих степени a2f(x) , b 2f(x) , af(x) bf(x) . | Однородное уравнение может быть первой степени и степни, больше чем вторая. | |
| af(x)> ag(x), где а>0, а≠1 или af(x)>ag(x), где а>0, а≠1 | af(x) >ag(x) 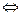  , где а>0, а≠1 или
af(x) >ag(x) , где а>0, а≠1 или
af(x) >ag(x) 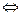  , где а>0, а≠1 , где а>0, а≠1
| Применяется для любого положительного основания, отличного от 1. | ||
| 6. | af(x) >b где а>0, а≠1 или af(x) <b где а>0, а≠1 | При b>0 af(x) >b 
| Применяется для любого положительного основания, отличного от 1. Если основание содержит переменную величину, то следует отдельно рассмотреть случай, когда основание равно 1, нулю, а так же отрицательно |   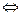 
|
| 7. | Aa2x+Bax+C>0, A≠0. | С помощью подстановки y=ax сводится к квадратному неравенству Ay2+By+C>0. | Применяется для неравенств, содержащих степени af(x) и a 2f(x) или af(x) и a-f(x) . | (⅓)2x-8∙(⅓) x -9>0, пусть (1/3)x =y, тогда данное неравенство будет иметь вид:
y2 -8y – 9>0,
решим это неравенство методом итервалов, получим y>9 или y <-1.
Возвращаясь к замене, получим (1/3)x >9 или(1/3)x <-1.
Решение первого неравенства: x < -2, x  (-∞;-2) (основание показательной функции 1/3 <1), второе неравенство решений не имеет.
Ответ: (-∞;-2). (-∞;-2) (основание показательной функции 1/3 <1), второе неравенство решений не имеет.
Ответ: (-∞;-2).
|
| Aa2x + Bax bx +Cb2x = 0, A≠0 | Однородное неравенства второй степени. Все члены левой части разделить на b2x | Применяется для неравенств, содержащих степени a2f(x) , b 2f(x) , af(x) bf(x) | Однородное неравенство может быть первой степени и степни, больше, чем вторая. |
Тестовые задания: решение показательных уравнений и неравенств(23)
| № | Задание | Ответы |
| 1. | Решите уравнение:3│x│=cos 
| 1.1; 2. -2; 3. 8; 4. 4; 5.0. |
Решите уравнение
│sin x + cos x│= 2│ sin x │+ 
| 1.1; 2. Æ; 3. 8; 4. 4; 5. -8. | |
Решите уравнение 2cos  = 5x+5-x = 5x+5-x
| 1.1; 2. -2; 3. 0; 4. 4; 5.2. | |
| Решите уравнение 2х+2 – 2-х = 4+2х - x2 | 1.1; 2. 0; 3.5; 4. 4; 5. -2. | |
| 8 – x 2x + 2 3-x-x = 0 | 1.1; 2. 0; 3.5; 4. 2; 5. -2. | |
| Решением уравнения 5х+12х=13х является: | 1.1; 2. 0; 3.5; 4. 2; 5. -2. | |
Решением уравнения =sinx2 является: =sinx2 является:
| 1.1; 2. Æ; 3. 8; 4. 4; 5. -8. | |
Решите уравнение
3x-2 + 32-x = 
| 1.1; 2. Æ; 3. 8; 4. 4; 5. 2. | |

| 1.[0;3]; 2.[ 1;3] | |
Найдите облать определения функции y= 
| 1.  ;
2. ;
2.  ;
3. ;
3. 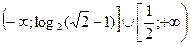 ;
4.[-1;1/2]
5.[1/2;1] ;
4.[-1;1/2]
5.[1/2;1]
| |
Сколько целых решений имеет неравенство

| 1.1; 2. 10; 3. 8; 4. 4; 5. 2 | |
Решите уравнение 
| 1.1; 2. 0,5; 3. 2; 4. 4; 5. 3 | |
Решите уравнении е 
| 1.1,5; 2. 0,5; 3. 1; 4. 4; 5. 3. | |
Найдите  , где x- меньший корень уравнения , где x- меньший корень уравнения 
| 1.1,5; 2. 0,5; 3. 1; 4. 4; 5. 6. | |
Решите уравнение 
| 1.1,5; 2.11; 3. 1; 4. 4; 5. 3. | |
Решите уравнение 
| 1.  2. Æ; 3).
2. Æ; 3).  4)-
4)-  ;
5) ;
5)  , где р , где р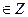
| |
Решите уравнение 
| 1.1,5; 2. 0; 3. 1; 4. 4; 5. 3. | |
Репшите неравенство 
| 1.[1/9;1]
2.  3.
3. 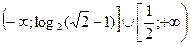 ;
4.[-1;1/2]
5.[1/2;1] ;
4.[-1;1/2]
5.[1/2;1]
| |
Решите уравнение 
| 1.1,5; 2. 10; 3. 1; 4. 4; 5. 3. | |
Решите уравнение 
| 1.1,5; 2. 10; 3. 16; 4. 4; 5. 3. | |
Решите уравнение 
| 1.  2) Æ; 3).
2) Æ; 3).  4)-
4)-  ;
5) ;
5)  , где р , где р 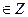
| |
Решите уравнение 
| 1.-1/3;3 2. 1;3. 3. 1;1/3. 4. -4; 5. 3. | |
Решите уравнение 
| 1.1,5; 2. 10; 3. 1; 4. 4; 5. 3. | |
Решите уравнение 
| 1.1,5; 2. 10; 3. 1; 4.2; 5. 3. | |
Решите уравнение 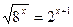
| 1.1,5; 2. 10; 3. 1; 4.2; 5. 3. | |
Решите уравнение 
| 1.1,5; 2. 10; 3. 1; 4.2; 5. 3. | |
Решите уравнение 
| 1. 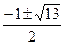 2.
2. 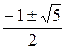 .
3. .
3.  ; ;  4.±1;
5..±2;
4.±1;
5..±2;
| |
Решите уравнение  . .
|  ; ; 
| |
Решите уравнение 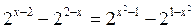
| 1. 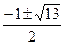 2.
2. 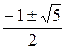 .
3. .
3.  ; ;  4.±1;
5..±2;
4.±1;
5..±2;
| |
Решите уравнение 
| 1.1,5; 2. 10; 3. 1; 4.2; 5.2. | |
Решите уравнение 
| 1.  2.
2. 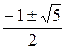 .
3. .
3.  ; ;  4.±1;
5. ±12;
4.±1;
5. ±12;
| |
Решите уравнение  . .
| 1.  2.
2. 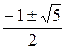 .
3. .
3.  ;
4.±1;
5. ±12; ;
4.±1;
5. ±12;
| |

| 1.[1/9;1]
2.  3. (2; +∞);
4.[-1;1/2]
5.[1/2;1]
3. (2; +∞);
4.[-1;1/2]
5.[1/2;1]
| |
Решите уравнение 
| 1.1,5; 2. 10; 3. 1; 4.2; 5. 0,5 | |
| Решите уравнение 2x 51/x=2·5 | 1.1, log25; 2.1. 3. log25; 4.±1; 5.2log25;; | |
| Решите уравнение 7x 41/x =7·4. | 1.1, log47; 2.1. 3. log47; 4.±4; 5. 1/2log47; | |
| (⅓)2x-8∙(⅓) x -9>0 | 1.[1/9;1]
2.  3. (2; +∞);
4.(-∞;2)
5.[1/2;1]
3. (2; +∞);
4.(-∞;2)
5.[1/2;1]
| |
Решите неравенство:

| 1.[1/2;1]
2.  3. (2; +∞);
4.(-∞;-1/2]
3. (2; +∞);
4.(-∞;-1/2]  [8;+∞)
5.[1/2;8] [8;+∞)
5.[1/2;8]
| |
Решите неравенство:

| ||
Решите неравенство: 
| 1.[1/3;1]
2.  3. (0; +∞);
4.(-∞;2)
5.[1/9;1]
3. (0; +∞);
4.(-∞;2)
5.[1/9;1]
| |
Решите неравенство: 
| 1.[1/2;3]
2.  3. (2; +∞);
4.(-∞;1)
5.[1/3;9]
3. (2; +∞);
4.(-∞;1)
5.[1/3;9]
|