Уравнение sinx = a, x- неизвестная переменная, a – некоторое постоянное число.
а) Если a>1 или a< -1, то уравнение sinx = a не имеет решений.
Например, уравнения sinx = 4, sinx = -2,4 не имеют решений.
б)Ecли a= 1, то решение уравнения: x= 
в) Ecли a= -1, то решение уравнения: x= -
г) Ecли a= 0, то решение уравнения: x=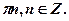 
д) Ecли |a|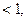 
то x=(-1)narcsina+πn, n 
.
Например, решение уравнения sinx = 0,3 записывается в виде:
x = (-1)narcsin0,3+πn, n .
Уравнение соsx = a, x- неизвестная переменная, a – некоторое постоянное число.
а) Если a>1 или a< -1, то уравнение cosx = a не имеет решений.
Например, уравнения cosx = 1,4, sinx = -2,5 не имеют решений.
б)Ecли a = 1, то решение уравнения: x= 
в) Ecли a= -1, то решение уравнения: x= 
г) Ecли a= 0, то решение уравнения: x= 
д) Ecли a 
то x= 
arccosa+2πn, n .
Например, решение уравнения cosx = 0,3 записывается в виде
x= arccos0,3+2πn, n .
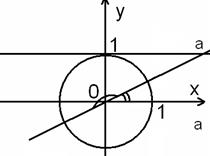
Уравнение tgx = a, x – неизвестная переменная, a – некоторое постоянное число.
Решение уравнения x = arctga + πn, n .
Например, решение уравнения tgx =3, будет x = arctg3 + πn, n .
Замечание: если a = 0, то x = πn, n .
Схема решения простейших тригонометрических уравнений
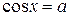
Нет корней 
Нет корней
■ 
■
♦ 
♦
● 
●
| 
| |
| 
|
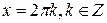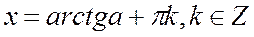
Примеры
Решите уравнение:
а) sinx = 3; б) sinx = -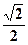 
; в) cosx = -2,3; г) cosx = - 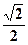; д) tgx = 
.
а) Так как 3>1, то решений нет. Ответ: решений нет.
б) x =(-1)karcsin(- )+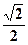 
x =(-1)k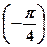 
+ 
x =(-1)k+1 
+ Ответ: (-1)k+1 +
в) Так как -2,3>1, то решений нет; Ответ: решений нет.
г) x= 
, x= 
;
Ответ: ;
д) tgx = , x = arctg + x = 
+ Ответ: +
3.Виды тригонометрических уравнений:
1. Уравнения, в которых можно выполнить замену переменной
Такие тригонометрические уравнения можно привести, например, к виду
af2(x)+bf(x)+c= 0,
где a,b,c – некоторые действительные числа,a ≠0, f(x)- одна из тригонометрических функций.
Например, 4sin2x +5 sinx+1 = 0.
Обозначим sinx = t, (1)тогда данное уравнение можно записать в виде:
4t2 +5t +1 = 0, это квадратное уравнение относительно t, найдем его корни.
D=9, t1= -1;t2=-0,25.
Подставим найденные значения t1 и t2 в равенство (1).
Получим простейшие тригонометричкские уравнения sinx =-1,sinx =- 0,25.
Решение первого уравнения x= - Решение второго уравнения
x =(-1)k+1arcsin0,25+
Ответ: - 
; (-1)k+1arcsin0,25+
Пример
Решить уравнение sin2 x + cosx +1= 0.
Решение
sin2 x + cosx +1= 0, заменяя sin2 x = 1- cos 2x, получим 1- cos 2x+ cosx +1= 0,
cos 2x - cosx -2= 0.
Обозначим cosx = t, (1)тогда данное уравнение можно записать в виде:
t2 -t -2 = 0, это квадратное уравнение относительно t найдем его корни.
D=9, t1= -1; t2 =2
Подставим найденные значения t1 и t2 в равенство (1).
Получим простейшие тригонометричкские уравнения cosx = -1, cosx = 2.
Решение первого уравнения x=
Второе уравнение решений не имеет, т.к. 2>1.
Ответ: 
,
2. Однородные тригонометрические уравнения.
Такие уравнения можно привести к виду a∙sin2x+bsinxcosx+ k∙cos2x= 0,
a,b,k – некоторые действительные числа, a≠0, k≠0.
Например, 4sin2x +5sinx cosx+cos2x = 0.Такие уравнения – однородные уравнения второй степени
Чтобы решить такое уравнение, надо:
1. Разделить почленно обе части уравнения на cos 2x ≠ 0,т.е.
4 
;
2.Выполнить преобразования: 4 
4tg 2x +5tgx+1=0.
3.Решить квадратное уравнение относительно tgx, tgx =t.
4t 2 +5t +1 = 0,
D=9, t1= -1;t2=- 0,25.
tgx = -1, tgx = - 0,25.
x = arctg(-1)+πk, 
или x = arctg(-0,25)+πn, 
,
x = - +πk, или x = - arctg 0,25+πn, .
Ответ: - +πk, ; - arctg0,25+πn,
Пример
Решить уравнение 4sin2x +sin2x -3 = 0.
Решение
Заменим в данном уравнении sin2x по формуле двойного аргумента на 2sinxcosx, а 3- на 3sin2x +3сos2x, т.к. sin2x +сos2x =1, получим:
4sin2x +2sinxcosx-3sin2x -3сos2x =0, sin2x +2sinxcosx-3сos2x =0.
Последнее уравнение – однородное. Решим его:
1. 
;
2. 
tg2x +2tgx - 3= 0.
3. tgx =t, t2 +2t - 3= 0. D=16, t1= 1;t2= -2.
tgx = 1, tgx = - 3.
x = arctg1+πk, или x = arctg(-3)+πn, ,
x = +πk, или x = - arctg 3+πn, .
Ответ: +πk, ; - arctg3+πn,
Для решения однородных уравнений можно использовать следующую таблицу:
1. Привести уравнение к виду 
2. Решить уравнение 
|
3. Уравнение вида asinx+bcosx=c
Чтобы решить уравнение такого вида (например,3sinx+4cosx=2), можно 1.Записать его в виде sin(x +t) =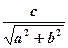 
(в нашем случае sin(x +t) = 
,
sin(x +t) = 
).
2.Решить простейшее тригонометрическое уравнение: sin(x +t) =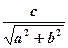
(в нашем случае sin(x +t) = , x+t =(-1)karcsin0,4 +πk, ;
x = (-1)k arcsin0,4 – t +πk, ;
3. Определить t, t = arctgb/a (в нашем случае t = arctg4/3);
4. Записать ответ: x = (-1)k arcsin0,4 – arctg4/3+πk, .
Пример
Решите уравнение 2sinx +cosx = 1.
Решение
1. sin(x +t) = 
, sin(x +t) = 
;
2. x+t = (-1)k arcsin +πk, , x = (-1)k arcsin -t+πk, ;
3. t = arctg1/2;
4. , x = (-1)k arcsin -arctg0,5 +πk, /
Для решения уравнения вида 
, где 
можно использовать следующую таблицу:
| Уравнение | Равносильное уравнение | Дополнительное условие |
|
| 
|  ,
 ,
 .
|
Если левая часть тригонометрического уравнения 
содержит лишь одно из выражений 
или 
и функцию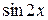 
(или произведение 
), то, вводя новую переменную 
или 
и учитывая, что 
, 
, приходим к уравнению относительно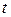 
.
Для решения тригонометрических уравнений данным способом можно использовать таблицу
5. Некоторые другие виды тригонометрических уравнений
Примеры
Решите уравнение:
а) sin(3x+ ) = 0,5; б) sin2x + cosx = 0; в)sinx + cosx = 0
Решение
а) sin(3x+ ) = 0,5.
Обозначим 3x+ = t, получим: sint = 0,5- простейшее уравнение, его решение t =(-1)k 
+ Заменим t на 3x+ , получим 3x + = (-1)k +
Решим это уравнение относительно х:
3x = - + (-1)k + 
, разделим все члены правой части уравнения на 3, получим x = - 
+ (-1)k 
+ 
.
Ответ: - + (-1)k + .
б) sin2x – cosx = 0.
Заменим в данном уравнении sin2x по формуле синуса двойного аргумента на 2sinxcosx, получим
2sinxсos + cosx = 0.
Затем вынесем cosx за скобки, получим: cosx (2sinx-1) = 0,
откуда сosx = 0 или 2sinx -1=0;
x = 
или sinx = 0,5;
x = или x = (-1)n +
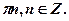
Ответ: ; (-1)n +
в) sinx + cosx = 0.
Это уравнение можно рассматривать как однородное уравнение первой степени относительно функций синуса и косинуса. Чтобы решить это уравнение:
Разделим почленно обе части уравнения на cosx,получим:
2.Выполним преобразования:
tgx +1 = 0, tgx = -1.
3.Решим простейшее уравнение tgx = -1, x= 
Ответ:
6.Уравнения, решаемые с помощью применения свойств ограниченности тригонометрических функций
  
 
|
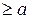
1)  .
Так как  и 
для  , то уравнение
равносильно системе
Так как  , то
 — корень исходного уравнения.
|
|
Ответ: .
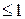
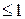2) 
=2
Ответ: .