Проверочный тест:
1. Найдите:
а) sinx и tgx, если сosx =1/5, x 
[- π/2;0].
б) cosx, если tgx=2, x [ π; 3π/2].
2. а) Найдите sin(α+β), если sinα =3/5, а cosβ=⅓, α [π/2; π], β [0; π/2],
б) Упростите: 
.
3. а) Найдите: сos 210°; sin(-135°); tg (11π/6).
б) Упростите: 
.
4. а) Найдите sin2α; cos2α; tg2α, если tgα=5, α [0; π/2]
б) Найдите sinx, cosx, tgx, если cos2x= 
, x [π/2; π].
5. Упростите: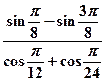 
Ответы:
1. а) - 
; б) 
; 2.а) 
; б) 1; 3. а) - 
; - 
; - 
; б) 
; 4. а) 
- 
; - 
; б) 
; - 
; - 
; 5. - 
.
Улучшите свои знания
Тригонометрические функции одного и того же аргумента
1. sin²x + cos²x =1
- сумма квадратов синуса и косинуса одного и того же аргумента равна 1.
По этой формуле, зная значения синуса какого – нибудь угла (например, sinx =1/3), можно найти косинус этого же угла (cos²x =1- sin²x =1-(1/3)²=
=1-1/9=8/9, cosx=±2 
. Знак cosx зависит от того, в какой четверти
находится угол х.
Зная значения косинуса какого – нибудь угла, по этой формуле можно
найти синус этого же угла: найдем sinx, если сosx=1/5, x [- π/2;0];
sin²x=1-cos²х =24/25, sinx=-2 
, так как при x [- π/2;0] sinx<0.
2. 
где x ≠ π/2+ πn, n – любое целое число; где x ≠ πn, n – любое целое число
3. ctg²x +1 = 1/ sin²x, x≠ πn, n – любое целое число.
По этой формуле, зная значения котангенса какого - нибудь угла (например, ctgx =4), можно найти синус этого же угла, т.е. sinx.
(sinx= 
= 
, знак зависит от того, в какой четверти находится угол х)
4. tg²x +1 = 1/ cos²x, x≠π/2+ πn, n – любое целое число.
По этой формуле, зная значения тангенса какого – нибудь угла (например,
tgx =5, x [π/2; π]), можно найти косинус этого же угла, т.е. cosx.
(cosx = - 
= 
, знак «- », так как при x [π/2; π] cosx<0)
5. tgx∙ctgx=1, x≠ 
, n – любое целое число.
Пример:
Найдите значения всех тригонометрических функции угла x, если
tgx =0.75, x [π; 3/2π]
Решение
Из формулы tgx∙ctgx=1 найдемctgx=1/tgx =1:0.75 = 4/3.
Из формулы tg²x +1 = 1/ cos²x найдем cosx = - 
, знак «- », берется потому, что при x [π; 3/2π] cosx<0.
Из формулы 
найдем sinx = cosx∙tgx =- 0.8∙0.75 = -0.6.
Формулы сложения тригонометрических функций
1. Синус суммы двух углов:
sin(x +y) =sinxcosy + sinycosx
2. Синус разности двух углов:
sin(x -y) =sinxcosy - sinycosx
3. Косинус суммы двух углов:
cos(x+y) = cosxcosy – sinx siny
4. Косинус разности двух углов:
cos(x-y) = cosxcosy + sinx siny
5. Тангенс суммы двух углов:
tg(x+y) = 
, где
x+y≠ π/2+ πn, x≠π/2+πk, y≠π /2+πm, n,m,k – целые числа.
6. Тангенс разности двух углов:
tg(x-y) = 
, где
x- y≠ π/2+ πn, x≠π/2+πk, y≠π /2+πm, n,m,k –целые числа.
Примеры:
а) Найдите cos(x+y), если sinx =3/5, а cosy=⅓, x [π/2; π], y [0; π/2].
Решение
Запишем формулу cos(x+y) = cosx cosy – sinx siny. В правой части этой формулы значения cosx и siny не известны.Найдем их:
cosx = - 
= 
, siny = 
= 
.
Подставим найденные значения в формулу cos(x+y) = cosxcosy – sinx siny, получим: cos(x+y)= 
.
б) Упростите выражение: .
Решение
Замечаем, что в числителе представленной дроби записана правая часть формулы косинуса разности двух углов, т.е.
cos 110°cos40° +sin 110° sin 40° = cos(110° – 40°)= cos70°.
В знаменателе представленной дроби записана правая часть формулы синуса разности двух углов, т.е.
sin 35°cos15° – cos35°sin15°=sin(35° – 15°) = sin 20°. Тогда получим:
= 
, cos 70° = sin20°,т.к. 20° дополняет 70° до 90°.
Формулы приведения
Формулы приведения позволяют от тригонометрических функций аргумента + α, перейти к тригонометрическим функциям аргумента α.
Например, sin(π/2+α) = cos α, cos(π+α) = - cos α.
Правило:
а) если в формуле приведения (например, cos(5π/2+α)) аргумент α
прибавляется к числу π/2(или вычитается из числа π/2), взятого нечетное
число раз(в нашем случае 5раз), то название функции меняется на
«кофункцию»: синус- на косинус, косинус- на синус, тангенс- на котангенс (в нашем случае название функции косинус изменится на синус);
б) если в формуле приведения (например, cos(3π +α)) аргумент α прибавляется к числу π/2(или вычитается из числа π/2), взятого четное
число раз(в нашем случае – 6 раз, 3π =6· π/2), то название функции не меняется;
в) знак приведенной функции определяется по знаку приводимой функции в соответствующей четверти, считая угол α острым (так как 5π/2+α принадлежит второй четверти, а во второй четверти косинус принимает отрицательные значения, то cos(5π/2+α)=-sinα; угол 3π +α принадлежит третьей четверти, а в третьей четверти косинус принимает отрицательные значения, значит, cos(3π +α)=-cos α).
Примеры
а) Найдите: сos 210°; sin(-135°); tg (11π/6).
Решение.
сos 210°= cos(180˚+30˚) =-cos30˚=- 
/2, так как 180˚=90˚·2(π/2 взято четное число раз), то название функции не меняется; угол 180˚+30˚ находится в третьей четверти, значения косинуса в ней отрицательны, поэтому перед приведенной функцией поставлен знак «- ».
sin(-135°) =-sin(90° +45°)=- cos45° = -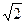 
/2
tg (11π/6) = tg (2π- π/6)=-tg π/6=- /3
б) Упростите выражение: 
Решение.
= 
= 
=
= 
= 