(f'(x) = 0, 3x3-3x2 -6x = 0, x(x2 –x -2) =0, x1=0, x2 =2, x3 =-1, f(-1)=1,25, f(0)=0, f(2)=-8)
| x | (- 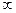 ;-1) ;-1)
| -1 | (-1;0) | (0;2) | (2; 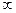 ) )
| ||
| f’(x) | - | + | - | + | |||
| f(x) | убывает | 1,25 min | возрастает | 0-max | убывает | -8 min | возрастает |
- Используя результаты исследования, построить график.
На первом рисунке отметили точки пересечения графика функции с осями координат (пункты исследования 4 и 5).
На втором рисунке отметили экстремумы (пункт исследования 6).
На третьем – достроили график на промежутках возрастания и убывания функции (пункт исследования 6).



Применение производной для нахождения наибольшего и
Наименьшего значений функции.
Чтобы найти наибольшее и наименьшее значение функции f(x) на отрезке [a;b], (например, f(x) = -2x3 - 6x2 +5 на [ -1;1]) надо:.
1.Найти производную функции; (f'(x) = -6x2 -12x)
2. Найти точки, в которых производная равна нулю или не существует (критические точки функции); (f'(x) = 0;
-6x2 -12x=0,-6x(x+2)=0, x =0, x=-2)
3.Выбрать из этих точек те, которые принадлежит промежутку [a;b]; (только точка x =0 принадлежит промежутку
[ -1;1])
4.Вычислить значения функции в выбранных критических точках и на концах промежутка [a;b]; (f(0) =5; f(-1) =1;
f(1) =-3.)
Выбрать из этих значений наибольшее и наименьшее.
Наибольшее значение функции f(x) = -2x3 -6x2 +5 на [ -1;1] равно 5;
наименьше значение функции f(x) = -2x3 -6x2 +5 на [ -1;1] равно-3.
Применение производной для определения мгновенной скорости.
Если движение точки задано уравнением s(t), то в момент времети to
Скорость ее движения равна s'(t).
Например, прямолинейное движение точки задано уравнением
s(t) = 2t2 -8t -10м. Найдите скорость движения в момент времени t =3c.
Решение.
1.Вычислим s' (t)=(2t2 -8t -10)' = 4t -8.
2.Найдем значение s' (2), s' (3)= 4∙3-8 =4(м/c)– это скорость движения в момент времени 3с.
Применение производной к решению геометрических задач
Чтобы найти тангенс угла наклона касательной, к оси абсцисс проведенной к графику функции f(x) в точке (x0 ; f(x0), нужно
1.Найти производную функции (f'(x));
2.Найти значение производной в точке x0 (f'(x0));
3. Полученное значение будет равно тангенсу угла наклона, т.е. tgα = f'(x0).
Например: Найдите угол наклона к оси абсцисс касательной, проведенной к графику функции у = x2 в точке с абсциссой x0 = 0,5.
1. Найдем производную функции f(x) = x2, f''(x) = 2x.
2. Найдем значение производной в точке x0 = 0,5, f''(0,5) = 1.
3. Тангенс угла наклона касательной к оси абсцисс равен 1.
Можно определить угол наклона касательной к оси абсцисс:
он равен 45˚, т.к. tg45˚ = 1.
8.Уравнение касательной к графику функции f(x) в точке (x0 ; f(x0))
Чтобы составить уравнение касательной к графику функции f(x) в точке (x0 ; f(x0)), надо
1.Записать уравнение касательной к графику функции в точке f(x) в точке (x0 ; f(x0)):
у =f'(x0)x- f'(x0)x0 + f(x0);
2. Найти значение производной в точке x0 (f'(x0));
3. Найти значение функции в точке x0 (f(x0));
Подставить найденные значения в уравнение пункта 1.
Например:
Составьте уравнение касательной, проведенной к графику функции
y = x3+1 в точке (1; 2).
1. Запишем уравнение касательной:
у =f'(x0)x- f'(x0)x0 + f(x0);
2.Найдем значение производной в точке x0 =1:
f'(x) = 3x2, f'(1)=3;
3.Найдем значение функции в точеке x0 =1: f(1) =2;
4. Подставим найденные значения в уравнение:
у =3x - 3∙1 + 2;
у =3x – 1- это уравнение касательной, проведенной к графику функции
y = x3+1 в точке (1; 2).