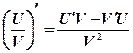,
в предположении, что производные U и Vсуществуют и V≠0.
Например,
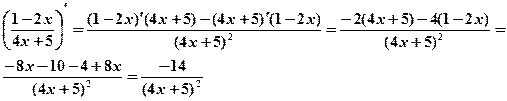
в)производная степени xα
(xα)'=αxα -1.
Например, (5x8)'= 5(x8)' = 40x7.
2.Производная функции в точке
Чтобы вычислить производную функции в точке, надо:
1.Найти производную функции по правилам.
2. В найденную производную подставить данное значение аргумента.
Например:
Найдите f'(2), если f(x) =3 x5.
1. f'(x)=(3x5)'=15x4
2. f'(2)=15∙24=240.
3.Производная сложной функции
Производная сложной функции f'(g(x)) равна производной промежуточной функци (y=g(x)), умноженной на производную функции (f'(y)).
f'(g(x)) = f'(y) g'(x).
Чтобы найти производную сложной функции, надо:
1.Определить функцию f(y);
2. Определить функцию y =g(x);
3. Найти f'(y) g'(x).
Замечание 3.1
f'(kx+b) =kf'(y), y=kx+в
Например:
Найдите ((1-3x)4)'
1.f(y) = y4
2.y=1-3x
3. 4(1-3x)3 (1-3x)' = -12(1-3x)3.
4.Производная тригонометрических функций
(sinx)'=cosx; (cosx)'= - sinx; tgx =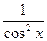 
; ctgx= 
.
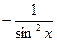Например, sin'(4x+7)=4cos(4x+7).
Примеры
Найдите производную функции а) f(x) = (2x +5)4; б) f(x) = (3x2 -7)(4x2+9);
в) f(x) =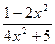 
; г) f(x) =3cos(2x-1); д) f(x) = 
.
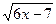Решение
а)Функция f(x) = (2x +5)4 сложная, вида f(kx+b). Найдем ее производную по замечанию 3.1:
((2x +5)4)' = 2∙4(2x+5)3 =8(2x+5)3.
б) Найдем производную функции (3x2 -7)(4x2+9) по правилу нахождения
производной произведения:
((3x2 -7)(4x2+9))' = (3x2-7) '(4x2+9) + (4x2+9)'(3x2-7) =6x(4x2+9) +8x(3x2-7) =
=24x3 -2x.
в) Найдем производную функции 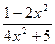по правилу нахождения
производной частного:
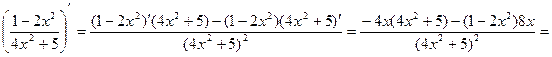
г) f'(x) =(3cos(2x-1))'= 3(cos(2x-1))', (постоянный множитель можно выносить за знак производной), далее 3(cos(2x-1))' = -3∙2sin(2x-1),
(производная cosy = - siny и f'(kx+b) = kf'(y), поэтому возникает коэффициент 2). Окончательно имеем: f'(x) = -6sin(2x-1).
д) f'(x) = (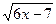)' = ((6x-7)0,5)' =0,5∙6(6x -7)0,5-1 =3(6x -1)-0,5,
для нахождения этой производной выполнили следующее:
|
|
1. представили квадратный корень в виде степени с показателем 0.5;
2. применили формулу для отыскания производной степени ((уt)'=tyt-1);
3. использовали замечание 3.1(появился множитель 6).
Наиболее часто встречающиеся ошибки
!Проверь, не делаешь ли ты так!
1.(1-2x)'≠ 2, верно будет так: (1-2x)'=-2.
2. (x-3)' ≠-3x-2, правильно будет так: (x-3) ' = -3x – 4.
3. sin' (3x-8) ≠ cos(3x-8), правильно будет так: sin'(3x-8) = -3cos(3x-8).
4. 
правильно будет так: 
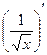= (x-0,5)' = - 0,5x -1,5 = 
.
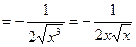Контрольный тест
1.Найдите производную функции:
а) f(x) = 3 
+4x3;
б) f(x) = 
в) f(x) = tg(2x+1) – x;
г) f(x) =(-x3 -2)(1- x4).
2. Вычислите f'(x0), если f(x) = (2x-8)5, x0 = 3;
3. Решите неравенство: f'(2) >x-5, если f(x) = sin(2x-4).
Тема5 Применение производной к решению задач
Проверочный тест:
1. Найдите промежутки монотонности функции y = x3-27x.
2. Найдите точки экстремума функции y = x3-27x.
3. Исследуйте функцию y = x3-3x2 на монотонность и экстремумы.
4. Исследуйте функцию y = 0,75x4 – x3 –3x2 и постройте ее график.
5. Найдите наибольшее и наименьшее значение функции
f(x) = – 2x3 –3x2 +4 на промежутке [-2; -0,5]
6. Прямолинейное движение точки задано уравнением
s(t) = 2t2 -8t -10 (s в метрах, t в секундах)
Найдите скорость движения в момент времени, равный 8 с.
7. Найдите угол наклона к оси абсцисс касательной, проведенной к
графику функции у = x2 в точке с абсциссой x0 = 0,5.
8. Составьте уравнение касательной, проведенной к графику функции
y = x3+1 в точке (1; 2).
Ответы:
1. На промежутках (-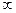 
; -3] и [3; 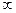) функция возрастает, на промежутке
[-3; 3] функция убывает.
2. x= -3 – точка максимума, x=3 –точка минимума.
3. На промежутках (- 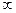; 0] и [2; 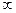) функция возрастает, на промежутке
|
|
[0; 2] функция убывает, x= 0 – точка максимума, x =2 –точка
минимума.
4. 
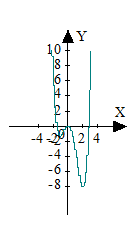
5. Наибольшее значение функции равно 8, наименьше значение функции
равно 3.
6.24м/c.
7. 45˚.
8. y = 3x – 1;
Улучшите свои знания