Если функция имеет положительную производную в каждой точке интервала (a;b), то она возрастает на этом интервале.
Если функция имеет отрицательную производную в каждой точке интервала (a;b), то она убывает на этом интервале.
Промежутки возрастания и убывания функции называются промежутками ее монотонности.
Если функция монотонна на интервале (a; b) и непрерывна в точках a и b, то она монотонна на отрезке[ a; b].
Чтобы найти промежутки монотонности функци f(x) (например, f(x)= x3-27x), надо:
- Найти D(f) (дляf(x)= x3-27x – это вся числовая прямая).
- Найти f'(x) ((x3-27x)' = 3x2 -27).
- Решить неравенсва
f'(x)> 0 (3x2 -27>0, 3(x2 -9)>0,x 
),
f'(x)< 0 (3x2 -27<0, 3(x2 -9)<0, x 
).
4.Записать ответ:
решения неравенства f'(x)> 0 – это промежутки возрастания,
(на промежутках (-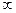 
; -3) и (3; 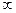) функция f(x)= x3-27x возрастает);
решения неравенства f'(x)< 0 –это промежутки убывания
(на промежутке (-3; 3) функция f(x)= x3-27x убывает).
Замечание. Так как f(x)= x3-27x непрерывна на области определения, то концы промежутков можно присоединить к промежуткам монотонности.
Применение производной для отыскания точек экстремума
(точек максимуиа и минимуиа) функции
Чтобы найти точки экстремума функции функци f(x) (например,
f(x)= x3-27x), надо:
1.Найти производную функции ((x3-27x)' = 3x2 -27).
2.Найти точки, в которых производная равна нулю или не существует f'(x) = 0, (3x2 -27=0, 3(x2 -9) = 0, x2 -9 = 0,(x-3)(x+3)=0, x=3, x=-3). f'(x) существует на всей области определения функции f(x)= x3-27x.
3.Проверить знак производной слева и справа от найденных точек и непрерывность функции в этих точек
4.Если функция непрерывна в точке, а производная меняет знак с «+» на «-» при переходе через эту точку, то эта точка – точка максимума
(x= -3, точка максимума).
5.Если функция непрерывна в точке, а производная меняет знак с «-» на«+» при переходе через эту точку, то эта точка – точка минимума
(x= -3, точка минимума).
Отыскание промежутков монотонности и точек экстремума функции.
Промежутки монотоности и точки экстремума чаще всего находят совместно.
Чтобы найти промежутки монотонности и точки максимума и минимума функции (например, y = x3-3x2), надо:
1.Найти область определения функции D(f) (дляf(x)= x3-3x2 – это вся числовая прямая).
2.Найти производную функции ((x3-3x2)' = 3x2 -6x).
Найти точки, в которых производная равна нулю или не
Существует
f'(x) = 0, (3x2 -6x=0, 3x(x -2) = 0, x=0, x=2). f'(x) существует на всей
области определения функции f(x)= x3-3x2.
Проверить знак производной слева и справа от
Найденных точек и непрерывность функции в этих
Точках
5.Заполнить таблицу:
| х | (- 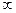;0)
| 0 - точка максимума | (0;2) | 2 -точка минимума | (2;+ )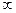
|
| f'(x) | + | - | + | ||
| f(x) | возрастает | 0, max | убывает | -4, min | возрастает |
Общая схема исследования функции и построения графика функции.
Общее исследование функции (например, y = 0,75x4 – x3 –3x2) можно выполнить по схеме:
1.Найти область определения функции (дляf(x)= 0,75x4 -x3 -3x2 это вся числовая прямая).
Установить четность или нечетность функции
(f(-x)= 0,75(-x)4 – (-x)3 –3(-x)2 =0,75x4 + x3 –3x2 ≠ f(x) ≠-f(x), функция не является ни четной, ни нечетной).
Установить периодичность функции.
(Функция y = 0,75x4 – x3 –3x2 не являетя периодической)
4.Найти нули функции(точки пересечения графика с осью OX), для этого решить уравнение f(x)=0. (0= 0,75x4 – x3 –3x2 , x2(0,75x2 – x –3)=0, x1=0, x2 ≈-1,4, x3≈ 2,8)
5. Найти точку пересечения графика с осью OY, для этого вычислить значение функции в точке 0, т.е. f(0). (f(0)= 0,75·04 – 03 –3·02 = 0)