!Проверь, не делаешь ли ты так!
1.  , правильно будет:
, правильно будет:  .
.
2.  при a <0, правильно будет:
при a <0, правильно будет:  .
.
3.  при a<0 и b<0, правильно будет:
при a<0 и b<0, правильно будет: 
4.  , правильно будет
, правильно будет  .
.
Контрольный тест
1.Решите уравнение:
а) 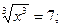 б)
б)  в)x4 =7; г) x5 =5.
в)x4 =7; г) x5 =5.
2.Упростите выражение:
 .
.
3.Сравните значения выражений:
 и
и 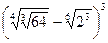 .
.
Свойства корня n- ой степени в таблицах(10) 
| № | Свойство | Применение | Примечание | Пример |
 , n- натуральное, большее единицы. , n- натуральное, большее единицы.
| Вычисление значений выражений, решениe иррациональных уравнений | Если n – нечетное, больше 1, то a может принимать отрицательные значения. | 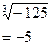
| |
 ,
m и к, целые, к >0, n- натуральное, большее единицы. ,
m и к, целые, к >0, n- натуральное, большее единицы.
| В тождественных преобразованиях, при вычислении значений выражений. | Если m и n нечетные, то может произойти сужение области определения выражений при переходе от левой части равенства к правой. | 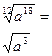
| |
 a ≥0; b≥0. a ≥0; b≥0.
| В тождественных преобразованиях, при вычислении значений выражений. | При a<0 и b<0, справедливо  ,где n- натуральное число. ,где n- натуральное число.
|

| |
 a ≥0; b>0. a ≥0; b>0.
| В тождественных преобразованиях, при вычислении значениий выражений. | При a<0 и b<0, справедливо  ,где n- натуральное число ,где n- натуральное число
| 
| |
 для любых натуральных m и к, неотрицательного числа a. для любых натуральных m и к, неотрицательного числа a.
| В тождественных преобразованиях, при вычислении значениий выражений. | Для нечетных показателей степени и корня число a может быть отрицательным | 
| |
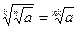 , для любых натуральных n и к, неотрицательного числа a. , для любых натуральных n и к, неотрицательного числа a.
| В тождественных преобразованиях, при вычислении значениий выражений. | Показатели корня могу быть только натуральными числами | 
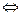    Ø Ø
| |
Для любого действительного числа a и для n – четного верно равенство:

| В тождественных преобразованиях, при решении уравнений и неравенств. | Если показатель степени – нечетное число, то верно равенство  . .
|  

| |
Для любого неотрицательного числа a и натурального n верно равенство:
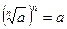
| В тождественных преобразованиях, при решении уравнений и неравенств. | Если показатель степени – нечетное число, то верно равенство 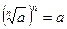 , при любом действительном a. , при любом действительном a.
|  , ,

| |

| В тождественных преобразованиях, при решении уравнений и неравенств | Целесообразно применять, если a2 –b есть полный квадрат | 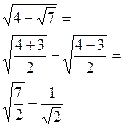
|
Тестовые задания: свойства корня n- ой степени(11)
| № | Задания | Ответы |
Вычислите значение выражения 
| а) 4; б) 8; в) 1; г) 2. | |
Вычислите значение выражения 
| а) 5; б) 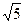 ; в) 25; г) ; в) 25; г) 
| |
Упростите выражение 
| а) 5a5; б) 2|a|5 + 3a 5 ; в) 2|a|5 - 3a 5 ; г) a 5 . | |
Результат упрощения выражения: 
| а) 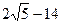 ; б) 4; в)1; г)2; ; б) 4; в)1; г)2;
| |

| а))8; б) 4; в)1; г) 0,5; | |
Результат упрощения выражения

|  ; б) ; б)  ; в) 1; г) 2 ; в) 1; г) 2  . .
| |
Результат упрощения выражения  равен
равен
| а)  + +  ; б) ; б)  + +  ; в) 2; г) 2 ; в) 2; г) 2  . .
| |
Равенство  верно при: верно при:
| а) x = 2; б) x = 0; в) x = -3; г) x = 3,5 | |
Равенство  верно при:
а) х = -111; б) х = -1; в) х = 0; г) х = 25. верно при:
а) х = -111; б) х = -1; в) х = 0; г) х = 25.
| а) х = -111; б) х = -1; в) х = 0; г) х = 25. | |
Равенство  верно при: верно при:
| а) x = -2; б) x = 5,2; в) x = 0, 2; г) x = 1,44; | |
Если  , то значение выражения , то значение выражения  равно: равно:
| а) 0,4; б) 5,2; в) - 4; г) 2,5 | |
Значение выражения  равно равно
| ||
Значение выражения  равно равно
| 1)  ;2)0
2) 1; 3) 6; 5) ;2)0
2) 1; 3) 6; 5)
| |
Если a >2, то результат упрощения выражения  равен равен
| 1) 
| |
Вычислите 
| 1)4  ; 2)22;
3)-22; 4) -4 ; 2)22;
3)-22; 4) -4  ; 5)0. ; 5)0.
| |
Результат упрощения выражения 
| 1)4с-2 d8; 2) 4d8; 3) с-2 d8; 4) с-2 d8; 5) с2 d 4;. | |
Значение числового выражения  равно равно
| 1)8  -20; 2)20;
3)-40; 4) -4 -20; 2)20;
3)-40; 4) -4  ; 5)0. ; 5)0.
| |
Значение выражения  равно равно
| 1)  ;2)0;
3) ;2)0;
3)  ; 4)2 ; 4)2  ;
5)- ;
5)- 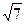
| |
Значение выражения  равно равно
| 1)  ;2)0;
3) ;2)0;
3)  ; 4)2 ; 4)2 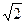 ;
5) ;
5) 
| |
Значение выражения  равно равно
| 1)  ;2)0;
3) ;2)0;
3)  ; 4)- ; 4)-  ;
5) ;
5) 
| |
Если  , то значение выражения , то значение выражения  равно равно
| 1)1/3;2)2/3; 3)-2/3; 4)1/6; 5)5/6. | |
Результат упрощения выражения 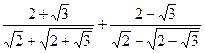 равен равен
| 1)  ;2)0;
3) ;2)0;
3)  ; 4) ; 4) 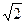 ;
5) ;
5) 
| |
Результат упрощения выражения  равен равен
| 1)  ;2)0;
3) ;2)0;
3)  ; 4)3 ; 4)3  ;
5) ;
5) 
| |
Если 1≤x≤2, то значение выражения  равно равно
| 1)  ;2)0;
3) ;2)0;
3)  ; 4)5 ; 4)5 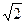 ;
5)2. ;
5)2.
| |
Результат упрощения выражения  равен равен
| 1)4  ; 2)14;
3)4; 4) -4; 5)0. ; 2)14;
3)4; 4) -4; 5)0.
| |
Результат упрощения выражения  равен
равен
| 1)  ;2)0;
3) ;2)0;
3)  ; 4) ; 4) 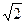 +5;
5) +5;
5)  +5 +5
| |
Результат упрощения выражения  равен
равен
| 1)4  ; 2)14;
3)4; 4) ; 2)14;
3)4; 4)  ; 5)0. ; 5)0.
| |
Результат упрощения выражения  равен: равен:
| 1) 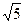 ; 2) ; 2)  ; 3) 2,125; 4) 2; 5. ; 3) 2,125; 4) 2; 5.
| |
Результат упрощения выражения  равен равен
| 1) 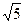 ; 2) ; 2)  ; 3) 2; 4) ; 3) 2; 4)  ; 5.1. ; 5.1.
| |
Результат упрощения выражения
 равен равен
| 1) 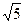 ; 2) ; 2)  ; 3) 2; 4) ; 3) 2; 4)  ;5. ;5. 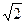 . .
| |
Результат упрощения выражения
 равен равен
| 1) 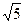 ; 2) ; 2)  ; 3) 2 ; 3) 2  ; 4) ; 4)  ;5. ;5. 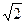 . .
| |
Результат упрощения выражения
 равен равен
| 1) 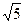 ; 2) ; 2)  ; 3) 2 ; 3) 2  ; 4) ; 4)  ;5.3+ ;5.3+ 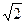 . .
| |
Упростите выражение 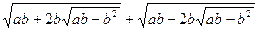 при b > a/2
при b > a/2
| 1)2b; 2)  ;
3) ab 4)2b+a;5. b ;
3) ab 4)2b+a;5. b 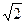 . .
| |
Упростите выражение  при b>0 при b>0
| 1)2b; 2) 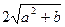 ;
3) ab 4)2b+a;5. b ;
3) ab 4)2b+a;5. b 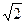 . .
| |
Упростите выражение

| 1) 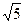 ; 2) ; 2)  ; 3) 2; 4) ; 3) 2; 4)  ; 5. ; 5. 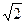 . .
| |
Упростите выражение

| 1) 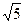 ; 2)3; 3) 2; 4) ; 2)3; 3) 2; 4)  ; 5. ; 5. 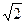 . .
| |
Результат упрощения выражения

| 1)2b;
2) 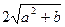 ;
3) ab;
4)2ax;
5. ;
3) ab;
4)2ax;
5. 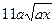 . .
| |
Результат упрощения выражения
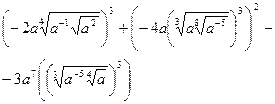 равен равен
| 1)2b;
2) 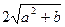 ;
3) ab;
4)2ax;
5. ;
3) ab;
4)2ax;
5. 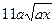 . .
| |
Результат упрощения выражения
 равен равен
| 1.  2.
2. 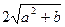 ;
3. ab;
4.2ax;
5. ;
3. ab;
4.2ax;
5.  . .
| |
Результат упрощения выражения
 равен равен
| 1.  2.
2.  ;
3. ;
3.  ;
4.3;
5. ;
4.3;
5. 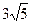 . .
|
Свойства функции 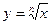 (12)
(12)
| Функции Свойства функции |
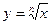 , n – четное , n – четное
| 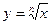 , n – нечетное , n – нечетное
|
| Область определения (D) | [0; +∞) | (-∞; +∞) |
| Множество значений(E) | [0; +∞) | (-∞; +∞) |
| Четность или нечетность функции | Нечетная | |
| Знаки функции | Функция неотрицательна на всей области определения | 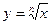 >0, если >0, если  ; ;
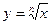 <0, если <0, если 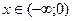
|
| Нули функции | x= 0 | x=0. |
| Промежутки возрастания | Функция возрастает на всей области определения | Функция возрастает на всей области определения |
| Промежутки убывания | - | - |
| Наибольшее значение | Не существует | Не существует |
| Наименьшее значение | y = 0 при x =0 | Не существует |
| Графики | 
| 
|
Тестовые задания: свойства функции 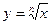 (13)
(13)
| № | Задание | Ответ |
Графику функции y =  принадлежит точка: принадлежит точка:
| a)(9; 3); b) (16;4) c) (9; -3); d) (16;-4). | |
Значение функции y =  при значении аргумента x = - 4
при значении аргумента x = - 4 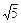 +9
равно: +9
равно:
| a) - 2 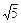 +3;
b) 2 +3;
b) 2 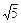 - 3; c) - 3; c) 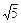 - 2;
d) 2 - - 2;
d) 2 - 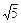 ; ;
| |
Множество значений функции
y = 2  +5 равно: +5 равно:
| a) (0; + ∞); b) [0; + ∞); c) [5; + ∞); d) (0; 5); e) (5; + ∞); | |
В облаcть определения функции
y =  входят значения аргумента, равные: входят значения аргумента, равные:
|
а)  ;
b) ;
b)  ; c) ; c) 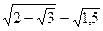 ;
d) ;
d)  e)
e)
| |
Множество значений функции
y = - 2  +5 равно: +5 равно:
| а) (- ∞; 5]; b) (-∞;0); c) [5; + ∞); d) (-5; 0); e)(- ∞;5); | |
Возрастающей на множестве всех действительных чисел является функция: 
| 
| |
Убывающей на множестве всех действительных чисел является функция: 
| 
| |
| Верным для всех действительных значений переменной x является неравенство: | 
| |
| Верным для всех действительных значений переменной x является неравенство: | 
| |
| Верным для всех значений x из области определения функции f(x) является неравенство f(x+3)>f(x), если: | 
| |
В облаcть определения функции
y =  входят значения аргумента, равные: входят значения аргумента, равные:
| а)  ;
b) ;
b)  ; c) ; c)  ;
d)arcsin(-1/3); e) cos(-2). ;
d)arcsin(-1/3); e) cos(-2).
| |
Найдите область определения функции 
| а) (- ∞; -5]; b) (-∞;0); c) [-5; + ∞); d) (-5; -3); e)[-5; -3]; | |
| Верным является неравенство: | 

| |
Найдите область определения функции 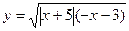
| а) (- ∞; -5]; b) (-∞;-3); c) [-5; + ∞); d) (-5; -3); e)[(∞; -3]; | |
Найдите область определения функции 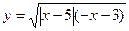
| а) (- ∞; -5]  ; b) (-∞;-3);
c) [-5; + ∞); d) (-5; -3);
e)(-∞; -3] ; b) (-∞;-3);
c) [-5; + ∞); d) (-5; -3);
e)(-∞; -3]  ; ;
| |
| Функция является возрастающей на области определения: | a);d) 
| |
Найдите область определения функции

| а) (- ∞; 0)  ; b) (-∞;-3);
c) [0;5) ; b) (-∞;-3);
c) [0;5)  (5; + ∞); d) (-5; -3);
e) (-∞; -3] (5; + ∞); d) (-5; -3);
e) (-∞; -3]  ; ;
| |
Найдите область определения функции 
| а) (- ∞; -5]; b) (-∞;-3); c) [-5; + ∞); d) [3; 5]; e)(-∞; -3]; | |
Найдите область определения функции 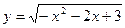
| а) (- ∞; -5]; b) (-∞;-3); c) [-5; + ∞); d) [3; 5]; e)[-3;1]; | |
Найдите множество значений функции 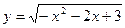
| а)(0;4]; b) (1;2); c) [1; 2); d) [0; 2]; e) [0;1]; |
Решение иррациональных уравнений и неравенств в таблицах (14)
| № | Вид уравнения (неравенста) | Метод решения | Применение | Примечение |

| Если a≥0, то x =a2n; если a < 0, то решений нет. |  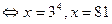
| 
| |

| x= a2n+1 | 
| 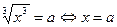
| |

|
Уравнение вида  равносильно системе равносильно системе
 . .
|

| Уравнение этого вида можно решить, возводя обе части уравнения в степень 2n и последующей проверкой корней подстановкой в данное уравнение   5-x2 = (1-x)2 5-x2 = (1-x)2  .
Проверка: x=-1, .
Проверка: x=-1,  равенство верное, значит x=2 – корень данного уравнения.
x=2, равенство верное, значит x=2 – корень данного уравнения.
x=2,  равенство неверное, значит x=2 – не корень данного уравнения. равенство неверное, значит x=2 – не корень данного уравнения.
| |

| Уравнение вида  равносильно системе равносильно системе
 . .
| 
| Уравнение этого вида можно решить, возводя обе части уравнения в степень 2n и последующей проверкой корней подстановкой в данное уравнение | |

| Уравнение вида  Равносильно совокупности
Равносильно совокупности

|   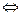 x=1 x=1
| Можно использовать условие равенства нулю произведения нескольких мноожителей | |

| 1.Можно возвести обе части уравнения в квадрат дважды с последующей проверкой. 2.Можно обе части уравнения умножить на выражение, сопряженное левой части. | 1. 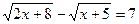     . Проверка: . Проверка:
 , значит, x = 4 не корень данного уравнения. , значит, x = 4 не корень данного уравнения.  , значит, x = 284 корень данного уравнения.
2. , значит, x = 284 корень данного уравнения.
2.
| Можно применить свойства функций.
Пример: Решить уравнение
 . .
 ,
функция y = ,
функция y = 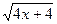 - возрастает на области определения, а функция
y= 4+ - возрастает на области определения, а функция
y= 4+  убывает на области определения. Следовательно, если данное уравнение имеет корень, то только один.
Легко угадывается корень x= 3. убывает на области определения. Следовательно, если данное уравнение имеет корень, то только один.
Легко угадывается корень x= 3.
| |

| Можно возвести обе части уравнения в квадрат дважды с последующей проверкой найденых корней | 2 
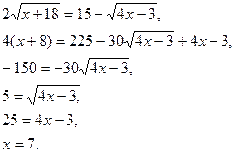 Проверка: Проверка:
 Значит, значение x =7 является корнем уравнения.
Значит, значение x =7 является корнем уравнения.
| Можно использовать свойства функций:
заметим, что функция y =2  возрастает на всей области определения, поэтому, если данное уравнение имеет корень, то только один.
Найдем его среди целых чисел, не больших 7. Как раз 7 – подходит, по теореме о единственности корня – 7 – единственный корень данного уравнения. возрастает на всей области определения, поэтому, если данное уравнение имеет корень, то только один.
Найдем его среди целых чисел, не больших 7. Как раз 7 – подходит, по теореме о единственности корня – 7 – единственный корень данного уравнения.
| |

| Если f(x) + g(x)=m, то можно сделать замену:

|    
| Если f(x) и g(x), одномонотонные, то уравнение  имеет только один корень, который можно подобрать.
Например, имеет только один корень, который можно подобрать.
Например,
 .
Функция y= .
Функция y=  возрастает на множестве всех действительных чисел, следовательно, уравнение возрастает на множестве всех действительных чисел, следовательно, уравнение
 имеет не более одного корня. Легко определяется,что x= 6 имеет не более одного корня. Легко определяется,что x= 6
| |

| При a>0 неравенство  равносильно
неравенству
0≤x<a2n равносильно
неравенству
0≤x<a2n
| 
| Неравенство со знаком «больше» справедливо при всех a<0. При a≥0 решениями будут x≥a 2n | |

| Неравенство вида
 равносильно следующей совокупности неравенств:
равносильно следующей совокупности неравенств: 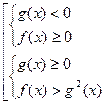
|    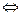 x x  (-∞; 1) (-∞; 1)
| Неравенства такого вида можно решать графически,
 . Для этого построим графики функций
f(x) = . Для этого построим графики функций
f(x) =  , и g(x) = x.
Решениями неравенства будут те значения x, для которых первый график расположен выше второго, т.е. x , и g(x) = x.
Решениями неравенства будут те значения x, для которых первый график расположен выше второго, т.е. x  . .

| |

| Неравенство вида
 равносильно системе
неравенств
равносильно системе
неравенств

|  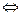
 
| 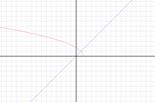 Неравенство можно решить с помощью графиков функций
Неравенство можно решить с помощью графиков функций  и y=x. и y=x.
| |

| Если a≥0, то
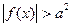
|  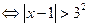 
| При a≤0, неравенство справедливо для всех x из области определения функции f(x) | |

| 
| 
| Можно использовать замену данного выражения на знакосовпадающее с ним | |

| Если a≥0, то

| 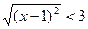  
| При a<0, неравенство не имеет решения | |

| 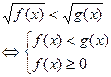
| 
| Можно использовать замену данного выражения на знакосовпадающее с ним. | |

| Можно решить методом интервалов. |  >4.
Найдем нули функции
y = >4.
Найдем нули функции
y =  , т.е. решим уравнение , т.е. решим уравнение  =4.
Получим x =3. Эта точка разбивает область определения функции y = =4.
Получим x =3. Эта точка разбивает область определения функции y =  , на два промежутка, определим знак функции в каждом из них, получим ответ (3; +∞) , на два промежутка, определим знак функции в каждом из них, получим ответ (3; +∞)
| Если f(x) и g(x), одномонотонные, то можно использовать свойства функций:
заметим, что функция y =  возрастает на всей области определения, а при x=3 принимает значение, равное 4, следовательно, для x>3 неравенство будет верным. возрастает на всей области определения, а при x=3 принимает значение, равное 4, следовательно, для x>3 неравенство будет верным.
| |

| Можно решить методом интервалов. |  < 4,
найдем нули функции
y = < 4,
найдем нули функции
y =  , т.е. решим уравнение , т.е. решим уравнение  = 4
Получим x =12. Эта точка разбивает область определения функции y = = 4
Получим x =12. Эта точка разбивает область определения функции y =  , на два промежутка. Определим знак функции в каждом из них, получим ответ [11; 12) , на два промежутка. Определим знак функции в каждом из них, получим ответ [11; 12)
| Если f(x) и g(x), одномонотонные, то можно использовать свойства функций:
заметим, что функция y =  возрастает на всей области определения, а при x=12 принимает значение, равное 4, следовательно, для 11≤x<12 неравенство будет верным. возрастает на всей области определения, а при x=12 принимает значение, равное 4, следовательно, для 11≤x<12 неравенство будет верным.
| |


| Используются неравенства о средних:
1.Неравенство между средним арифметическим и средним квадратичным двух положительных чисел:  a > 0, b>0. a > 0, b>0.
| Решите неравенство
 Заметим, что x = 2 – решение данного неравенства. Заменим левую часть неравенства на большее выражения при x > 2. По неравенству между средним арифметическим и средним квадратичным будем иметь:
Заметим, что x = 2 – решение данного неравенства. Заменим левую часть неравенства на большее выражения при x > 2. По неравенству между средним арифметическим и средним квадратичным будем иметь:
 
 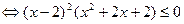 .
Последнее неравенство
справедливо только при x =2,поскольку это неравенство является следствием данного, то данное неравенство других решений не имеет. .
Последнее неравенство
справедливо только при x =2,поскольку это неравенство является следствием данного, то данное неравенство других решений не имеет.
| Решите неравенство

 Равенство достигается при условии равенства слагаемых, т.е. 17-x = 15+x, откуда x =1. Равенство достигается при условии равенства слагаемых, т.е. 17-x = 15+x, откуда x =1.
| |
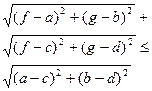
| Использование геометрических моделей |  длина отрезка AB, где A(x;y),
B(a;b) длина отрезка AB, где A(x;y),
B(a;b)
| Наименьшее(x+y), где (x;y) решение неравенства
 5 ≤ 5 ≤  .Геометрическая модель: AB+OB≤ OA. Равенство возможно, если точка A(x;y) принадлежит лучу OA. Наименьшее(x+y) = 4+3 = 7 .Геометрическая модель: AB+OB≤ OA. Равенство возможно, если точка A(x;y) принадлежит лучу OA. Наименьшее(x+y) = 4+3 = 7
| |

| Использовать свойства монотонности функции
y= 
| Если функции f(x) - g(x) одномонотонны на общей области их определения, то неравенство будет верным для всех значений переменной, из области определения функции, больших (в случае возрастания функций) и ли меньших (в случае убывания функций), корня уравнения 
|  >5
Заметим, что число x = 9- корень соответствующего уравнения.
Расмотрим функцию f(x) = >5
Заметим, что число x = 9- корень соответствующего уравнения.
Расмотрим функцию f(x) =  (2)
На всей области определения [0; +∞) функция возрастает.
Значит x=9 – единственный корень уравнения, а решение данного неравенства промежуток (9;+∞) (2)
На всей области определения [0; +∞) функция возрастает.
Значит x=9 – единственный корень уравнения, а решение данного неравенства промежуток (9;+∞)
|
Тестовые задания: иррациональные уравннеия и неравенства(15)
| № | Задание | Ответы | |||
Решите уравнение 
| 1.-1;2. 2. -2;3. 3. -1;4. 4. 4;2. 5. 1;2. | ||||
Решите уравнение 
| 1.-1;2. 2. -2;3. 3. -1;4. 4. -3;2. 5. 1;2. | ||||
Решите уравнение 
| 1.-1; 2. 2; 3. -4; 4. 4; 5. 3. | ||||
Решите уравнение 
| 1.-1; 2. -2; 3.2; 4. 4; 5. 3. | ||||
Решите уравнение 
| 1.-1; 2. -2; 3. 2; 4. 4; 5. 3. | ||||
Решите уравнение 
| 1.-1;2. 2. -2;3. 3. -1;1. 4. -3;2. 5. 1;2. | ||||
Решите уравнение 
| 1.-1; 2. -2; 3. 2; 4. 4; 5. 3. | ||||
Решите уравнение 
| 1.-1; 2. -2; 3. 1; 4. 4; 5. 3. | ||||
Решите уравнение 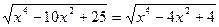
| 1.  2. -2;
3. ±1;
4. 4;
5. ±3.
2. -2;
3. ±1;
4. 4;
5. ±3.
| ||||
Решите уравнение 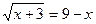
| 1.-1; 2. -2; 3. 6; 4. 4; 5. 3. | ||||
Решите уравнение 
| 1.-1/2;2. 2. -2;/2. 3. -1/2;`1/2. 4. -3/2;1/2. 5. 1/2;2. | ||||
Решите уравнение 
| 1.-1/2;1 2. -2;/2. 3. -1/2;`1/2. 4. -3/2;1/2. 5. 1/2;2. | ||||
Решите уравнение 
| 1.1; 2. -2; 3. 6; 4. 4; 5. 3. | ||||
Решите уравнение 
| 1.1; 2. -2; 3. 6; 4. 4; 5. 3. | ||||
Решите уравнение 
| 1.1; 2. -2; 3. 6; 4. 5; 5. 3. | ||||

| 1.1; 2. -2; 3. 6; 4. 4; 5.3. | ||||
Решите уравнение 
| 1.-1;1;3. 2. 1;-2;3. 3. -1;1;2. 4. -3;2;5. 5. 1;2;5. | ||||
Найдите наименьший корень уравнения

| 1.1; 2. -2; 3. 6; 4. 4; 5. -8. | ||||
Найдите наибольший корень уравнения 
| 1.1; 2. -2; 3. 8; 4. 4; 5. -8. | ||||
Решите уравнение
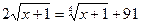
| 1.2400; 2. 2500; 3. 730; 4. 728; 5. 8. | ||||
Решите уравнение 
| 1.1; 2. -2; 3. 8; 4. -4; 5. -8. | ||||
Решите уравнение 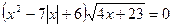
| 1.-23/4;-1;1;6 2. 1/4;-2;3;5. 3. -1;1;2;6. 4. -3;2;5;7/4. 5. 1;2;5/4;6. | ||||
Решите уравнение 
| 1.3; 2. -2; 3. 8; 4. -4; 5. -8. | ||||
Решите уравнение 
| 1.-109; 80 2. -180;36. 3. 109;90. 4. -109;-80. 5. 100;80. | ||||
Решите уравнение 
| 1. 2; 2. -2; 3. 8; 4. -4; 5. -8. | ||||
Решите уравнение 
| 1. 2401; 2.49; 3. 7; 4.27; 5. 125. | ||||
Решите уравнение  
| 1. 
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-02-13 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |