1.Решить неравенство: 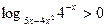
Решение

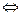
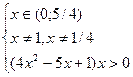
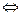 x
x 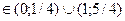 .
.
2.Решить неравенство: 
Решение



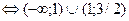
3.Решить неравенство: 
Решение
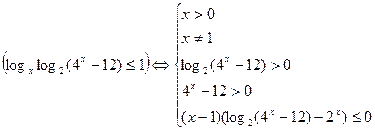
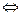

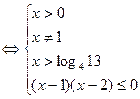

4. Решить неравенство:

Решение
Заметим, что выражение 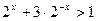 для
для 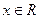 (
( , по свойству среднего арифметического и среднего геометрического).
, по свойству среднего арифметического и среднего геометрического).
Поэтому данное неравенство равносильно неравенству 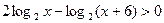 .
.
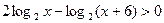
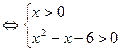
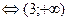 .
.
5. Решить неравенство
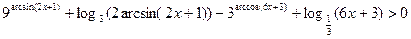
Решение
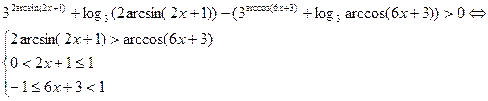
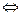
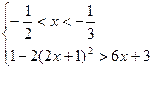
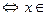
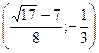
6.Найти сумму натуральных решений неравенства 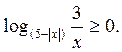
Можно решить это неравенство по аналогии с предыдущими неравенствами, используя правила замены выражений на совпадающие с ними по знаку:
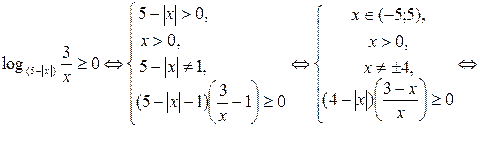

Натуральные решения 1; 2; 3. Их сумма равна 6.
Свойства логарифмов в таблице (24)
| № | Свойство, определение | Применение | Примечание | Пример |
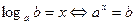 , где , где
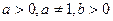
| Для вычисления значений логарифмов | Можно использовать для представления числа в виде логарифма по любому основанию | 2= log9 81 | |
Основное логарифмическое тождество
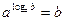 ,
b>0, a>0, a≠1. ,
b>0, a>0, a≠1.
| Для упрощения выражений | Можно использовать для представления любого положительного числа в виде степени с любым положительным основанием, отличным от 1 | 3= 5log5 3 | |
| logab + logac = logabc, где b>0, c>0, a>0, a≠ 1. | Для преобразований выражений, в уравнениях и неравенствах | При переходе от левой части равенства к правой область определения может расшириться. | log210= 1 + log25 | |
| logab - logac = loga (b: c), где b>0, c>0, a>0, a≠ 1. | Для преобразований выражений, в уравнениях и неравенствах | При переходе от левой части равенства к правой область определения может расшириться | lg 2=lg(10:5) 1 - g5 | |
| logabn =nloga b, где b>0, a>0, a≠ 1. | Для преобразований выражений, в уравнениях и неравенствах | При переходе от левой части равенства к правой область определения может сузиться | log2(x-2)4 = 4log2|x-2| | |
Формула перехода от одного основания логарифма к другому
logab= 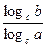 , где b>0, a>0, a≠ 1, с>0, c≠ 1. , где b>0, a>0, a≠ 1, с>0, c≠ 1.
| Для преобразований выражений, в уравнениях и неравенствах | При решении уравнений и неравенств, как правило, следует прейти к одному и тому же основанию логарифма. |
log29 = 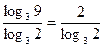 . .
| |
Формула замены основания логарифма на его число
logab =  , b>0,
b ≠1,a>0, a≠ 1, , b>0,
b ≠1,a>0, a≠ 1,
| Для преобразований выражений, в уравнениях и неравенствах |
Можно использовать неравенство |logab+  |≥2, b>0, a>0, a≠ 1, |≥2, b>0, a>0, a≠ 1,
| log29 = 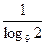 . .
| |
logarx= 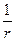 log a x, x>0, a>0, a log a x, x>0, a>0, a  . .
| Для вычислений и преобразований выражений | Для перехода к меньшему основанию логарифма | log 4x= 1/2log 2 x, | |
logarxr=log a x, x>0, a>0, a  . .
| Для перехода к другому основанию логарифма, вычислений и преобразваний | При переходе от одной части равенства к другой область определения может измениться | ||
clogab = blogac, a>0, a  , b>0, c>0, b , b>0, c>0, b  , c , c  . .
| Для перехода к одному основанию логарифма, при вычислениях, преобразованиях, в решениях уравнений и неравенств | Если равенство содержит переменные, то учесть область определения |
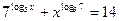
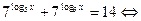
 =7 =7 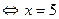
| |
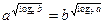 , a>0, a , a>0, a  , b>0, b , b>0, b  . .
| Для перехода к одному основанию логарифма при вычислениях, преобразованиях, в решениях уравнений и неравенств | Если равенство содержит переменные, то следует учесть область определения |

| |
| logab 2n =2nloga |b|, где b>0, a>0, a≠ 1. | Для преобразований выражений, в уравнениях и неравенствах | Если равенство содержит переменные, то следует учесть область определения | log4 (x-2) 2 =2log4 |x-2| | |
(logab >0) 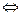 ((a-1)(b-1)>0), a>0, a ((a-1)(b-1)>0), a>0, a  , b>0. , b>0.
| При решении неравенств | Учитывать область определения |
(logx (x+4) >0) 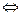 ((x-1)(x+3)>0), x>0, x
((x-1)(x+3)>0), x>0, x  , x+4>0. , x+4>0.
| |
(logab <0) 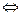 ((a-1)(b-1)<0), a>0, a ((a-1)(b-1)<0), a>0, a  , b>0. , b>0.
| При решении неравенств | Учитывать область определения | (logx (x+4) <0) 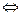 ((x-1)(x+3)<0), x>0, x
((x-1)(x+3)<0), x>0, x  , x+4>0. , x+4>0.
| |
logab - logac <0) 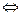 ((a-1)(b-c)<0), a>0, a ((a-1)(b-c)<0), a>0, a  , b>0, c >0 , b>0, c >0
| При решении неравенств | Учитывать область определения | 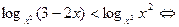
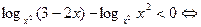 
| |
logab - logac >0) 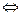 ((a-1)(b-c)>0), a>0, a ((a-1)(b-c)>0), a>0, a  , b>0, c >0 , b>0, c >0
| При решении неравенств | Учитывать область определения | 
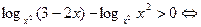 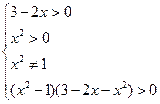
| |
logaa = 1, a>0, a  , ,
| При решении уравнений, неравенств | Учитывать область определения | 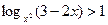 , ,
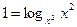
| |
loga1 = 0, a>0, a  , ,
| При решении уравнений, неравенств | log51 = 0, log31 = 0 | ||
logaa n =n a>0, a  , ,
| При решении уравнений, неравенств | log55 4 =4 |
Тестовые задания: применение свойств логарифмов(25)
| № | Задание | Результат |
Расположите в порядке возрастания значения выражений:
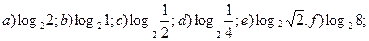
| a)-1; b) 2; c) ½; d)0; e) -2; f)3 e),a), d),c),b), f). | |
| Представьте число 3 в виде логарифма по основанию a) 3; b) 2; c) ½; d) 10; e)1/3; f)a | a)3= log 3 27; b) 3= log 2 9; c) 3= log 1/21/8; d) 3= lg1000; e) 3= log 1/31/27; f) 3= log a a3 | |
| Представьте в виде степени: a) с основанием 5 число 2; b) с основанием 6 число 7; c)с основанием 4 число 9; d) с основанием 7 число 15 e) с основанием 10 число 2; f) с основанием 1/2 число 6; | a)  b)
b) 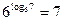 c) 9 = 4log4 9;
d) 15 = 7log7 15;
e) 2=
c) 9 = 4log4 9;
d) 15 = 7log7 15;
e) 2= 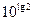 ;
f) 6= ;
f) 6= 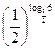
| |
Найдите значение выражения
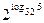
| 1)  ; 2) 25;
3) 6;
4) -5/4;
5) 4; ; 2) 25;
3) 6;
4) -5/4;
5) 4;
| |
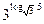
| 1)  ; 2) 25;3) 6;
4) -5/4;5) 4; ; 2) 25;3) 6;
4) -5/4;5) 4;
| |
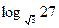 ; ;
| 1)  ; 2) 25; 3) 6;
4) -5/4;5) 4; ; 2) 25; 3) 6;
4) -5/4;5) 4;
| |
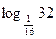 ; ;
| 1)  ; 2) 25;3) 6;
4) -5/4;5) 4; ; 2) 25;3) 6;
4) -5/4;5) 4;
| |
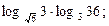
| 1)  ; 2) 25; 3) 6;
4) -5/4; 5) 4; ; 2) 25; 3) 6;
4) -5/4; 5) 4;
| |
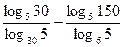 ; ;
| 1)  ; 2) 2;3) 6;
4) -5;5) 1; ; 2) 2;3) 6;
4) -5;5) 1;
| |
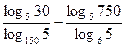 ; ;
| 1)  ; 2) 2;3) 6;
4) -5; 5) 1; ; 2) 2;3) 6;
4) -5; 5) 1;
| |
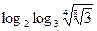 . .
| 1)  ; 2) 2;3) 6;
4) -5; 5) 1; ; 2) 2;3) 6;
4) -5; 5) 1;
| |
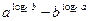 ; ;
| 1)0; 2) 2;3) 6; 4) -5; 5) 1; | |
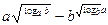 ; ;
| 1)0; 2) 2;3) 6; 4) -5; 5) 1; | |
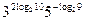
| 1)9; 2) 2;3) 6; 4) -5; 5) 1; | |
Пусть  Выражение log6 2
равно: Выражение log6 2
равно:
| 1)a/(a-1); 2) 1-a; 3) (1-a)/(2a); 4) 3(1+a); 5)- 1; | |
Найдите 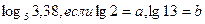
| 1)a-2b-2/(a-1); 2) 1-a; 3) (1-a)/(2a); 4) 3(1+a); 5)- 1; | |
Найдите 
| 1)a-2b-2/(a-1); 2) 1-a; 3) (1+a)/(2a+b); 4) 3(1+a); 5)- 1; | |
Пусть  Найдите: log 300 75
Найдите: log 300 75
| 1)(a+2ab)/(2+a+2ab); 2) 1-a; 3) (1+a)/(2a+b); 4) 3(1+a); 5)- 1; | |
Пусть  Найдите:
Найдите: 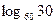
| 1)(a+2ab)/(2+a+2ab); 2) 1-a; 3) (1+a+ab)/(2+a+ab); 4) 3(1+a); 5)- 1; | |
Известно, что  . Вычислите . Вычислите 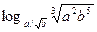
| 1)(1-  2) 1;
3) (2+
2) 1;
3) (2+  4) 3(1+
4) 3(1+  ); 5) ); 5) 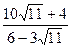 ; ;
| |
Известно, что 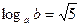 . Вычислите . Вычислите 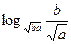
| 1) 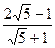 2) 1-
2) 1- 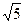 ;
3) 1;
4) 3(1+- ;
3) 1;
4) 3(1+- 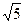 );5) );5) 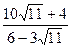 ; ;
| |
Определите верные неравенства
a) 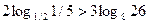 b)
b)  c)
c) 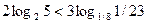 d)
d) 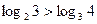 e)
e) 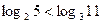 f)
f)  g)
g)  h)
h) 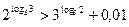
| 1.b,d,g. 2.a,b,f; 3.f,g,h; 4d,e,h; 5.a,f,h | |
Значение выражения 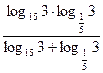 равно: равно:
| 1) 0; 2) 1
3) 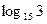 ; 4) ; 4) 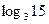 ;
5) -1 ;
5) -1
| |
Пусть  Какое из следующих выражений Какое из следующих выражений 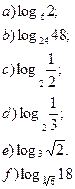 равно 3(1+a)? равно 3(1+a)?
| 1.b. 2. f; 3. h; 4d; 5.a. | |
Пусть  Выражение Выражение 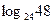 равно равно
| 1)a/(a-1); 2) 1-a; 3) (1-a)/(2a); 4) 3(1+a); 5)- 1; | |
Результат упрощения выражения 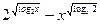 равен равен
| 1) 2; 2) log2x; 3) 0; 4) 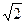 ; 5) другой ответ ; 5) другой ответ
|
Свойства логарифмической функции(26)
| Свойства функция | y = lоga x, a >1 | y = lоga x, 0 <a < 1 |
| Область определения (D) | D(lоga x) =(0;+ ∞) | D(lоga x) =(0;+ ∞) |
| Множество значений (E) | E(lоga x) =(- ∞;+ ∞) | E(lоga x) =(- ∞;+ ∞) |
| Нули функции | lоga x =0 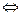 x=1 x=1
| lоga x =0 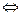 x=1 x=1
|
| Знаки функции | logax > 0 при x>1 logax < 0 при 0<x<1. | logax<0 при x >1 logax >0 при 0<x<1. |
| Промежутки возрастания | y = lоga x при a>1 возрастает на всей областиопределения. | |
| Промежутки убывания | y = lоga x при 0<a<1убывает на всей области определения. | |
| Графики | 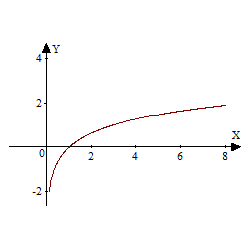
| 
|
Тестовые задания на применение свойств логарифмической функции(27)
| № | Задание | Ответ |
| Найдите область определения функции y=log3 (5 + 4x - x2 ) | 1.(-1;5);
2. [-1;5);
3. [-1;5];
4.(-∞;-1)  (5;+∞)
5..(-∞;-1] (5;+∞)
5..(-∞;-1]  [5;+∞) [5;+∞)
| |
| Найдите область определения функции y= logx+1 (2-x) | 1.(-1;2);
2. [-1;0);
3. [-1;2];
4.(-1;0)  (0;2)
5..(-∞;-1] (0;2)
5..(-∞;-1]  [2;+∞) [2;+∞)
| |
| Найдите множество значений функции y=log3 (5 + 4x - x2 ) | 1.(-1;2);
2. [-1;0);
3. [-1;2];
4.(-1;0)  (0;2)
5. (-∞;2] (0;2)
5. (-∞;2]
| |
| Наибольшее значение функции y=log3 (2+ 2x - x2 ) | 1)0;2)4;3)2;4)1; 5)1/9. | |
| Наименьшее значение функции y=log0,5 (3+ 2x - x2 ) | 1)0;2)4;3)-2;4)1; 5)1/4. | |
Больше единицы значение функции 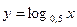 при x, равном: при x, равном:
| 1)64;2)4;3)2;4)1; 5)1/16. | |
Больше единицы значение функции 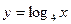 при x, равном: при x, равном:
| 1)64;2)4;3)2;4)1; 5)1/16. | |
| Только неотрицательные значения принимает функция: | 1.y=log1/3 (5 + 4x - x2 ); 2. y=log3 (5 + 4x + x2 ); 3. y=log3 (3 + 4x -x2 ); 4. y=log1/3 (3 + 4x -x2 ); 5. y=log1/2 (3 + 4x -x2 ). | |
| 7. | Решите уравннеие 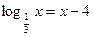
| 1)0;2)4;3)3;4)1; 5)1/9. |
| 8. | Решите уравннеие 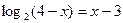
| 1)0;2)4;3)3;4)1; 5)1/9. |
| 9. | Решите уравннеие 
| 1)2;2)4;3)3;4)1; 5)1/9. |
Решите неравенство 
| 1. (1;7)  (7;+∞);
2. [1;7);
3. [1;2];
4.(1;7) (7;+∞);
2. [1;7);
3. [1;2];
4.(1;7)  (7;79)
5..(-∞;-1] (7;79)
5..(-∞;-1]  [7;+∞) [7;+∞)
| |
Решите неравенство 
| 1)0;2)4;3)-2;4)-1; 5)1/9. | |
Решите уравннеие 
| 1)0;2)π;3)3π;4)1; 5)3. | |
Решите уравннеие 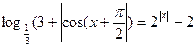
| 1)0;2)π;3)3π;4)1; 5)3. | |
Решите уравннеие 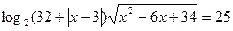
| 1)0;2)π;3)4;4)1; 5)3 | |
Решите уравннеие 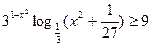
| 1)0;2)π;3)3π;4)1; 5)3. | |
Решите уравннеие 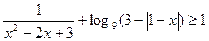
| 1)0;2)π;3)3π;4)1; 5)3. | |
Решите уравннеие 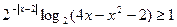
| 1)0;2)2;3)3π;4)1; 5)3. | |
Корень уравнения 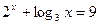 принадлежит промежутку принадлежит промежутку
| 1) (-3;1]; 2) [-1;2); 3) (-10;0]; 4) (-10;3]; 5) [0;3) | |
Наименьший корень уравнения 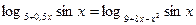 равен
равен
| 1) -2; 2) -0,5; 3) π/2; 4) 8; 5) другой ответ | |
Наименьшее неотрицательное число из области определения функции
y = 
| 1).1;2) π; 3) 2; 4) 2π; 5) 0. |
Решние логарифмических уравнений и неравенств в таблицах(28)
| № | Вид уравнения, неравенства | Метод решения | Применение | Примечание | |
| loga f(x)= loga g(x) а>0, а≠1 |
loga f(x)=
loga g(x)
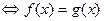 , где а>0, а≠1, g(x) > 0, f(x) > 0. , где а>0, а≠1, g(x) > 0, f(x) > 0.
| Применяется для любого положительного основания, отличного от 1. | При решении уравнения могу появиться посторонние корни, поэтому следует сделать проверку решений. | ||
| loga f(x)= = b где а>0, а≠1 | loga f(x)=
= b 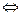 f(x)=a b f(x)=a b
| Применяется для любого положительного основания, отличного от 1. | 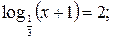
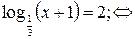 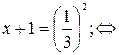 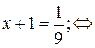 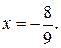
| ||
| A loga 2 f(x) +B loga f(x)= +C=0, A≠0. | С помощью подстановки y= loga f(x) сводится к квадратному уравнению Ay2+By+C=0. | Применяется для уравнений, содержащих loga 2 f(x) и loga f(x) или loga f(x) и loga -1 f(x). | Подстановка может быть применена к уравнению 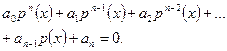 p(x)= loga f(x) p(x)= loga f(x)
| ||
| Уравнения, решаемые функциональным методом | f(x)= g(x) | Если f(x) возрастает, а g(x) не возрастает на их общей области определения, то уравнение f(x)= g(x) имеет не более одного корня. | 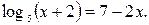 Так как
Так как 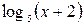 — возрастающая функция (основание больше единицы) и — возрастающая функция (основание больше единицы) и 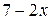 — убывающая, то уравнение — убывающая, то уравнение 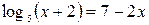 может иметь не более одного корня. Методом подбора его легко найти может иметь не более одного корня. Методом подбора его легко найти 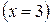 . .
| ||
| Уравнения, решаемые методом логарифмирования | Переменная величина под знаком логарифма и в основании степени | При условии, что обе части уравнения положительны, обе части уравнения можно логарифмировать | 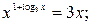 Область определения:
Область определения: 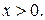
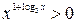 и и 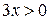 при при 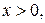 значит, логарифмируем по основанию 3. значит, логарифмируем по основанию 3.
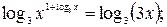 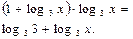 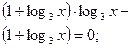 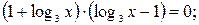
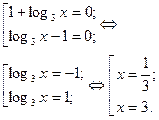
| ||
| 6. | loga f(x)> >loga g(x), а>0, а≠1; loga f(x)< <loga g(x) а>0, а≠1 | Применить замену данного выражения на знакосовпадающее с ним | Применяется для решения неравенств, содержащих переменную в основании | 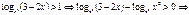
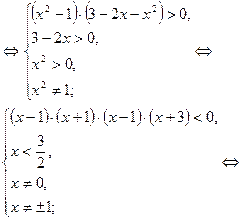 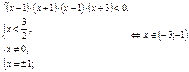
| |
| 7. | A loga 2 f(x) +B loga f(x) +C >0, A≠0. A loga 2 f(x) +B loga f(x) +C <0, A≠0. | С помощью подстановки y= loga f(x) сводится к квадратному неравенству Ay2+By+C>0. (Ay2+By+C<0) | Применяется для неравенств содержащих loga 2 f(x) и loga f(x) или loga f(x) и loga -1 f(x). | log72 x + log7 x < 6; Обозначим log7 x через t, log7 x =t, тогда неравенство примет вид t2 + t<6; откуда -3<t<2. Учитывая то, что log7 x =t, получим неравенство -3<log7 x<2, 1/343<x <49. Решением данного неравенства служит промежуток (1/343;49) | |
Тестовые задания: простейшие логарифмические уравнения и неравенства (29)
| № | Задание | Ответы |
Решите уравнение
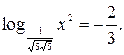 
| 1) 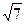 ; 2)2; 3); 4)0; 5) ; 2)2; 3); 4)0; 5) 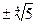 . .
| |
Решите уравнение
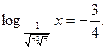
| 1) 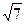 ; 2)2; 3); 4)0; 5) ; 2)2; 3); 4)0; 5) 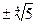 . .
| |
Решите уравнение
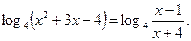
| 1) 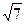 ; 2)2; 3); 4)-5; 5) ; 2)2; 3); 4)-5; 5) 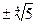 . .
| |
Число корней уравнения
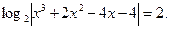
| 1)5; 2)2; 3)7; 4)0;5)6. | |
Число корней уравнения
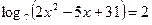 равно равно
| 1)3; 2)2; 3)7; 4)0;5)6. | |
Число корней уравнения

| 1)5; 2)2; 3)7; 4)0;5)6. | |
Решите уравнение
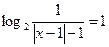
| 1.-0,5; 2,5; 2)2;3; 3)-7;1; 4)0;0,5 5)-2;2,5. | |
Решите уравнение
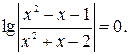
| 1)3; 2)2; 3)7; 4)0,55)6. | |
Решите уравнение

| 1.-3,25; 1,25; 2)2;3; 3)-7;1; 4)0;0,5 5)-2;2,5. | |
Решите уравнение
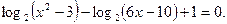
| 1)3; 2)2; 3)7; 4)0,55)6. | |
Решите уравнение
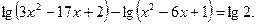
| 1)3; 2)2; 3)0; 4)0,55)6. | |
Число корней уравнения 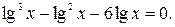

| 1)3; 2)2; 3)1; 4)0;5)4. | |
Решите уравнение
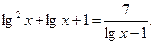
| 1)10; 2)2; 3)1; 4)100;5)0,1 | |
Число корней уравнения 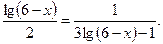
| 1)3; 2)2; 3)1; 4)2;5)0 | |
Решите уравнение
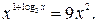
| 1. 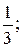 9; 2. 9; 2.  3;3)0; 1 4)0,09;35)9. 3;3)0; 1 4)0,09;35)9.
| |
Число корней уравнения 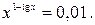
| 1)3; 2)2; 3)1; 4)4;5)0. | |
Число корней уравнения 
| 1)3; 2)2; 3)1; 4)0;5)4. | |
Число целых рашений неравенства: 
| 1)3; 2)2; 3)1; 4)0;5)4. | |
Наибольшее целое решение неравенства: 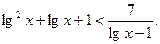
| 1)10; 2)2; 3)100; 4)99; 5) 1000 | |
Число целых решений неравенства 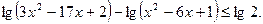
| 1)3; 2)2; 3)1; 4)4;5)0. |
Тестовые задания логарифмические уравнения и неравенства (30)
| № | Задание | Ответы |
| Решите уравнение log1/3(3+│sin x │) =2│x│-2 | 1)π; 2)2π; 3) π +2πn,n  Z; 4)0; 5) πn,n Z; 4)0; 5) πn,n  Z. Z.
| |
| Решите уравнение log22x + (x-1) log2x = 6-2x | 1)0,25; 2; 2)1; 1; 3) 2; 1; 4) 2; 2; 5)0,25;1. | |
Решите уравнение
log22 (x+y) – 2sinx 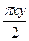 log2 (x+y) +1+
│y-1│=0 log2 (x+y) +1+
│y-1│=0
| 1)1; 2; 2)1; 1; 3) 2; 1; 4) 2; 2; 5)0,25;1. | |
Решите уравнение
3sin x = 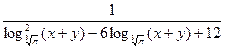
| 1)- 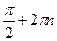 , , 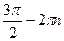 n n  Z;
2)2π; π;3) π +2πn, π +2πn, n Z;
2)2π; π;3) π +2πn, π +2πn, n  Z; 4)0; 0;5) πn,πn,n Z; 4)0; 0;5) πn,πn,n  Z. Z.
| |
| Решите уравнение: log2 (4x+1) log5 (4x+4)+ +log3 (4x+2) log4 (4x+3) = 2 log3 (4x+2) log5 (4x+4) | 1)¼. 2)1; 3) 2; 4) 2; 5)0,25; | |
Решите неравенство:
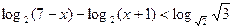
| 1.(1;7) 2)(1; +∞) 3) (7; +∞) 4) [1; +∞); 5) [7; +∞) | |
| 7. | Определите количество решений уравнения 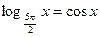 : :
| 1.4; 2.3; 3.5; 4.9; 5.1. |
Решить неравенство: 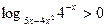
| 1. 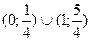 ;
2. ;
2. 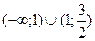 ;
3.[ 0;3] ;
3.[ 0;3]  (4;5);
4. (4;5);
4.  ;
5. ;
5. 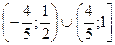
| |
Решить неравенство: 
| 1. 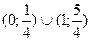 ;
2. ;
2. 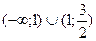 ;
3.[0;3] ;
3.[0;3]  (4;5);
4. (4;5);
4.  ;
5. ;
5. 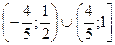
| |
Решите неравенство: 
| 1. 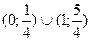 ;
2. ;
2. 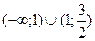 ;
3.[ 0;3] ;
3.[ 0;3]  (4;5);
4. (4;5);
4.  ;
5. ;
5. 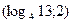
| |
Решите неравенство: 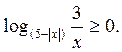
| 1.[1;3]
2. 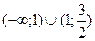 ;
3.[ 0;3] ;
3.[ 0;3]  (4;5);
4. (4;5);
4.  ;
5. ;
5. 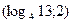
| |
Решите неравенство: 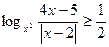 . .
| ||
Решите неравенство:
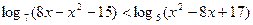
| 1.  ;
2. ;
2. 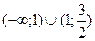 ;
3.[ 0;3] ;
3.[ 0;3]  (4;5);
4. (4;5);
4.  ;
5. ;
5. 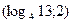
| |
Решите неравенство: 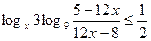
| ||
Решите неравенство: 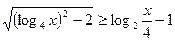
| 1.  2.
2. 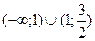 ;
3.[0;3] ;
3.[0;3]  (4;5);
4. (4;5);
4.  ;
5. ;
5. 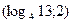
| |
Решите неравенство:
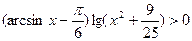
| 1. 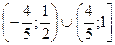 ;
2. ;
2. 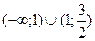 ;
3.[0;3] ;
3.[0;3]  (4;5);
4. (4;5);
4.  ;
5. ;
5. 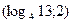
| |
Найдите сумму целых решений неравенства
 на промежутке [-3;3] на промежутке [-3;3]
| 1.4; 2.3; 3.5; 4.9; 5.1. | |
Решите неравенство:
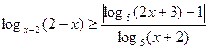
| 1) 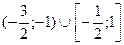 ;
2. ;
2. 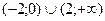 ;
3. ;
3. 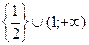 ;
4. ;
4. 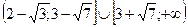 5.
5. 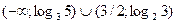
| |
Решите неравенство:
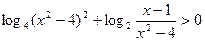
| 1) 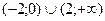 ;
2. ;
2. 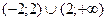 ;
3. ;
3. 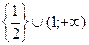 ;
4. ;
4. 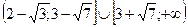 ;
5. ;
5. 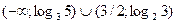
| |
Решите неравенство:
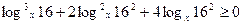
| 1) 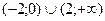 ;
2. ;
2. 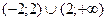 ;
3) ;
3)  ;
4. ;
4. 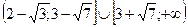 ;
5. ;
5. 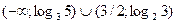
| |
Решите неравенство:
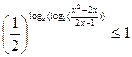
| 1) 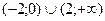 ;
2. ;
2. 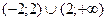 ;
3) ;
3)  ;
4. ;
4. 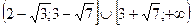 ;
5. ;
5. 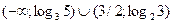
| |
Решите неравенство:
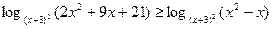
| 1) 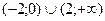 ;
2. ;
2. 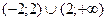 ;
3) ;
3)  ;
4. ;
4. 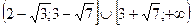 ;
5. ;
5. 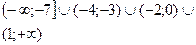
| |
Решите неравенство:
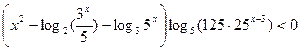
| 1.  2.
2. 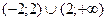 ;
3) ;
3)  ;
4. ;
4. 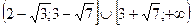 ;
5. ;
5.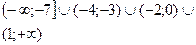
| |
| Определите число целых решений неравенства log2+x (6-│x│) ≥ 0 | 1) 6; 2.3; 3.5; 4.9; 5.1. | |
Решите уравнение
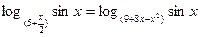
| 1.8, π/2; 5π/2. 2. 4, 5π/2. 3. π/2; 5π/2. 4. 5π/2. 5. 2, π/2. | |
| Решите уравнение: log9(37-12x)·log7-2x3 = 1. | 1.1; 2.3; 3.5; 4.2; 5.-1. | |
| lg sinx + lg cosx < 0 | 1.(2πn;π/2+2πn), n 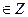 2. (4; 5π/)
3. (π/2; 5π/2).
4. 5π/2.
5.(1;π/2).
2. (4; 5π/)
3. (π/2; 5π/2).
4. 5π/2.
5.(1;π/2).
|
Дополнительные справочные материалы
| Данное выражение | Выражение, совпадающее по знаку с данным | Дополнительные условия |
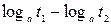
| 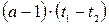
| 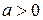 , ,  , , 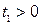 , , 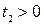
|
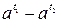
| 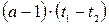
| 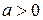 , , 
|
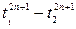
| 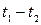
| 
|
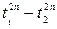
| 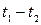
| 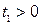 , , 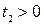 , , 
|
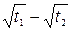
| 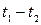
| 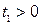 , , 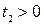
|
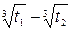
| 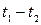
| — |
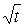
| 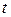
| 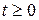
|

| 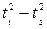
| — |

| 
| 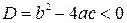
|
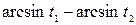
| 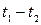
| 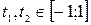
|
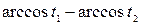
| 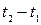
| 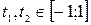
|
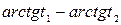
| 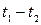
| — |
| Название формулы | Вид формулы | Применение | |
| Разность квадратов | a2 - b 2 = (a-b)(a+b) | Для разложения выражения на множители. | |
| Квадрат разности | (a - b) 2 = a 2 -2ab + b 2 | В тождественных преобразованиях. | |
| Квадрат суммы | (a + b) 2 = a 2 +2ab + b 2 | В тождественных преобразованиях. | |
| Куб разности | (a - b) 3 = a 3 -3a 2b +3a b 2 –b3 | В тождественных преобразованиях. | |
| Куб суммы | (a + b) 3 = a 3 +3a 2b +3a b 2 +b3 | В тождественных преобразованиях. | |
| Разность кубов | a3 - b 3 = (a-b)(a 2 +ab+b 2) | Для разложения выражения на множители. | |
| Сумма кубов |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-02-13 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд