ВРЕМЯ ЖИЗНИ ТОВАРА (УСЛУГИ)

 

В Главе II для моделирования рекламного процесса была сфор­мулирована бинарная модель рынка. Там же сказано, что хотя реаль­ность и сложнее любой модели, конструктивной альтернативы мате­матическому моделированию сложных процессов не существует. Однако эта модель может быть использована не только для планиро­вания рекламы, но и для анализа более широких маркетинговых за­дач, встающих при выборе стратегии рекламы. В этом параграфе мы рассмотрим некоторые вопросы маркетинга, оставаясь в рамках би­нарной модели.

Введем некоторые предварительные понятия.

 

· ПЛАНИРОВАНИЕ РЕК­ЛАМНОЙ КАМПАНИИ, методика которой описана выше,

- ограничено по времени и осуществляется в пределах одного РЕКЛАМНОГО ЦИКЛА.

· В этой главе мы будем рассматривать вопросы, связанные с анализом поведения спроса на достаточно больших промежутках времени, включающих много рекламных циклов. Поэтому для измерения вре­мени удобно ввести число рекламных циклов, которое обозначим m.

ЗАДАЧА:

Вначале рассмотрим следующую задачу:

НАЙТИ: суммарный спрос D(m),

ДАНО:

Известна динамика продаж за один цикл (m=1), обусловленная новыми покупателями.

РЕШЕНИЕ этой за­дачи позволит нам сделать весьма важные выводы о целях маркетин­говых мероприятий на конкретном временном интервале развития рынка.

 

· Введем параметр характеризующий процент ухода поку­пателей с рынка за один цикл.

Под уходом мы понимаем

- переход по­требителей на другой (конкурирующий) брэнд

- или вовсе отказ от по­требления товара (услуги) данной категории.

Смысл параметра и необходимость его введения вполне оче­видны. Действительно, трудно себе представить, что потребитель пользуется товаром (услугой) бесконечно долго; даже в том случае, когда потребитель пользуется товаром постоянно, вступает в силу физическое ограничение - человек не может жить вечно!

· Введем зависимость числа потребителей брэнда от числа реклам­ных циклов (от времени) — d(m) и вычислим суммарное число по­требителей, накопившихся ко времени m-ого цикла.

Оно, очевидно, дается суммой

 

 

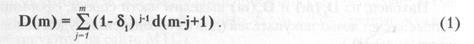
Действительно, в m-ый цикл мы (по определению) имеем:

- d(m) вновь пришедших потребителей,

- от m-1 цикла осталось (1- ) d(m-1) потребителей (т.к. d(m-l) - ушло),

- от m-2 цикла имеем, соот­ветственно (1- )`2 d(m-2) потребителей и т.д.

В итоге получаем фор­мулу (1).

 

· Теперь используем бинарную структуру рынка и разделим всех потребителей

§ на БРЭНДОВЫХ (индекс В)

§ и СВОБОДНЫХ (индекс L).

Для этого введем долю брэндовых потребителей Х(m) (процент позици­онирования рынка первых покупок). С учетом сказанного запишем:

 

 

Весь дальнейший анализ рынка будет связан с анализом след­ствий формул (2) и (3), который может быть проведен, если заданы функции d(m) и Х(m). Здесь мы ограничимся следующим модель­ным их представлением, позволяющим получить достаточно простые выражения, которые могут быть детально проанализированы:

 

Отметим, что спрос задан в относительных единицах (в едини­цах максимального числа новых потребителей за один цикл), а пара­метры X1 и d1 задают скорость насыщения доли позиционированных потребителей и спроса.

Учитывая (4), формулы (1)-(2) можно просуммировать, исполь­зуя выражение для суммы геометрической прогрессии:

 

 

где (m) = 1- (1- 1)`m.

Зная D(m) и DL(m), легко найти брэндовую часть спроса, поскольку DB(m) = D(m) - DL(m).

Наконец, из DL(m) и DB(m) выделим части спроса, сформиро­ванные за счет новых покупателей (для их обозначения будем исполь­зовать индекс 0):

 

 

С. 121

Подчеркнем еще раз, что DL0 и D B0 содержатся в DL и DB.

Принимая во внимание, что у части наших читателей громозд­кость полученных выражений может вызвать определенную «сла­бость», скажем, что нам еще повезло, что удалось просуммировать выражения (2) и (3) и получить такой простой вид формул! При m—>оо полученные выражения еще более упрощаются:

 

 

Выражения (8) записаны в единицах новых потребителей (мак­симальное число новых потребителей за цикл принята за 100%). Если умножить (8) на 1, то перейдем к единицам, в которых за 100% при­нята величина максимального рынка.

Параметр имеет фундаментальное значение в понимании ана­лиза тонкой структуры спроса.

Как видно из выражения (8), именно он определяет величину максимально возможных продаж. Далее бу­дет показано, что параметр вместе с еще одним параметром i (став­ка дисконтирования) определяет такую важную величину, как сто­имость брэнда.

ПРИМЕРЫ:

Теперь рассмотрим несколько примеров, иллюстрирующих прак­тическую ценность параметра .

Задача 1.

Рассчитать предельное число абонентов интернет-ком­пании, если максимальный месячный уровень подключений, опре­деляемый инфраструктурой продаж компании, составляет 30 новых абонентов. Средний срок пользования услугой равен приблизитель­но 5-ти годам.

Решение.

Сначала находим процент ухода абонентов в месяц:

=1/(5*12) = 1,6%.

Затем, используя (8), находим максимальное чис­ло абонентов

Dmax = 30/ , = 30/0,016 =1875 аб.

Ответ: Dmax =1875 аб.

Примечание: более точное значение для = 1,65% при расчете по схеме 1. п. 1.3.2.

 

Задача 2:

Рассчитать предельное число абонентов оператора со­товой связи МТС, если максимальный месячный уровень подключе­ний, на который может выйти компания в Москве, составляет 50 тыс. новых абонентов. Месячный процент ухода 2,25% (данные об уходе публикуются на сайте МТС).

Решение:

(мес)=2,25%;

Dmax= 50(т.мес)/ =2,2 млн. аб.

Ответ: D =2,2 млн. аб.

 

Задача 3:

Рассчитать месячное число продаж шампуня «Рыжая голова», осуществляемых только новыми (совершающими покупку первый раз) покупателями по России, если известно, что дистрибьюторская сеть реализует 100 тыс. шт. в месяц, а средний срок пользо­вания одним шампунем составляет 6 месяцев.

Решение:

(мес)=1/6=16,7%;

Do= Dmax =100 тыс. шт.* 0,167=16,7 тыс.шт.

Ответ: Do =16,7 тыс.шт.

Примечание: более точное значение для =15,4% при расчете по схеме 1. п. 1.3.2.

 

С. 122

ВЫВОД:

Таким образом,

· Зная процент ухода потребителей

- можно оце­нить максимальные продажи, если известно число новых покупате­лей

- или, наоборот, можно оценить число новых покупателей, зная мак­симальные продажи.

 

· В действительности параметр не является постоянной вели­чиной, а изменяется во времени (достаточно сложным образом). Эту зависимость можно учесть, подставив в выражения (1)-(3) соответ­ствующие функции (m), что приведет к существенному усложнению вычислений.

· Однако для практических расчетов вполне достаточно считать постоянной величиной, равной среднему значению (m).

 

СТОИМОСТЬ БРЭНДА

 

Ограничимся анализом экономического содержания понятия бренд.

С помощью введенного выше парамет­ра , можно определить такую важную характеристику, как сто­имость бренда. Практическая ценность простого и понятного опре­деления цены создаваемого (или имеющегося) бренда бесспорна, по­скольку вносит системность, осознанность в принятии решений по проведению маркетинговых мероприятий.

Методику расчета стоимости бренда мы схематически изобра­зили на рис. 42.

Рис. 42. Зависимость брэндовых продаж от времени (числа рекламных циклов) и схема вычисления стоимости брэнда.

 

Предположим, что инвестиции на создание брэнда позволили фирме

- за время mх

- занять долю рынка величиной dF.

Ко­нечно, мы не можем (как и никто другой) a priori предсказать дина­мику роста брэнда до величины dF Схематический вид возможных кривых изображен на рисунке. Для того чтобы знать действитель­ный ход кривой,

- нужно проводить замеры брэндовых продаж в про­межуточных точках (см. рис. 42).

- Это нужно также для коррекции проводимых инвестиций и для оценки времени выхода на стадию на­сыщения на брэндовом сегменте рынка.

Если после достижения доли dF каких-либо мероприятий по под­держанию достигнутого брэнда не проводится, то брэндовые прода­жи начнут уменьшаться (брэнд релаксирует, стареет). Будем считать, что в ПЕРИОД МОЛЧАНИЯ за каждый рекламный цикл уходит потре­бителей брэнда. Тогда уменьшение брэндовых продаж при m>mx про­исходит по закону (см. рис. 42):

 

 

Чтобы вычислить современную (на момент времени mх ) сто­имость dF будущих денежных потоков (продажи - брэндовые!), нуж­но осуществить процедуру дисконтирования с учетом изменения ве­личины денежных потоков (процедура дисконтирования схематичес­ки изображена на рис. 42). Для этого нужно просуммировать выра­жение

 

где

i - ставка дисконтирования за время, равное времени рекламного цикла;

к = (1- )/( +i) - коэффициент дисконтирования DF (сум­марных брэндовых продаж в денежном выражении — дохода, прибыли, выручки и т.д.).

С. 124

Оценка стоимости брэнда, производимая согласно выражению (10), вовсе не рассматривается нами как альтернатива уже существу­ющим методикам. Ее сила в простоте сравнительного анализа разных брэндов: для этого нужно знать только два параметра — и i.

Используя выражение (10) можно записать следующий крите­рий оценки эффективности инвестиций в брэнд:

 

где

Vo - затраты за цикл.

Согласно (11) затраты на создание брэнда должны быть меньше его стоимости.

ЗАДАЧИ:

Теперь проиллюстрируем практическую полезность оценки сто­имости брэнда (10) в рамках рассмотренных выше задач.

Задача 4. Рассчитать стоимость (в единицах прибыли) брэнда интернет-компании, если средняя прибыль от одного абонента состав­ляет $1 в месяц, =1,6% в месяц, стоимость денежных ресурсов на этом рынке оценивается в 20% годовых (1,6% мес.)

Решение: dBF =1875a6.*$l*(100%-l,6%)/(l,6%+l,6%) = $1875 * 30,75 = $57656.

Ответ: dBF = $57,7 тыс.

 

Задача 5:

1. Рассчитать удельную стоимость брэндов (в едини­цах выручки в расчете на одного абонента) операторов сотовой свя­зи МТС и Билайн в Москве, если средняя выручка от продажи ус­луг на одного абонента составляют:

- МТС - dMTC - 26,7$,

- Билайн - dБИ = 19,4$ (данные за 1кв. 2002г.);

2. Вычислить полную сто­имость брэндов, если

- число абонентов NMTC = 2,35 млн.; NБИ - 2,86 млн (данные за 1кв. 2002г.),

- МТС = БИ = 2,25% (в мес);

- стоимость денежных ресурсов на этом рынке оценивается в 12% годовых (1% в мес.)

Решение:

По пункту 1:

dMTC = $26,7*(100%-2,25%)/(2,25%+1%) = $26,7*30 = $801 (удель­ный брэнд или средний доход с одного абонента).

d мтс = Nмтс dмтс = 2,35млн.* $801= $1,9млрд. (суммарный брэнд).

dБИ = $19,4*(100% - 2,25%)/(2,25%+1%) = $19,4*30 = $582 (удель­ный брэнд).

d БИ = NБИ dБИ = 2,86млн.* $582 = $1,7млрд. (суммарный брэнд).

Примечание: Компания МТС в 2002 г. купила башкирского оператора «БМ-Телеком» за $70 млн. К моменту покупки ком­пания обслуживала 100 000 абонентов. Можно считать, что МТС оценила одного абонента в $700. Интересно, но наш расчет по формуле (10) дает аналогичный результат, если принять, что доход от одного абонента составляет $23.

Задача 6:

Рассчитать стоимость брэнда (в единицах чистой прибыли) шампуня «Рыжая голова», если известно, что

- дистрибьюторская сеть реализует 100 тыс. шт. в мес,

- =16,6% в месяц,

- чистая при­быль равна $0,2 с одного флакона.

- Ставка дисконтирования i = 16% в год (1,3% в мес).

Решение:

D0 = $0,2*100000(100%-16,6%)/(16,6%+1,3%) = $20 000*4.63 = $92600.

Ответ: dР.Г. = $92,6 тыс.

N.B!

Сделаем одно важное для выполнения оценок замечание:

- при расчете необходимо использовать величины и i в одних единицах (год, мес, нед.).

 

Рассмотрим еще один случай, когда процент ухода потребителей очень мал ( —> 0,) при этом время жизни товара (ус­луги) очень велико.

Тогда предельная стоимость брэнда определя­ется только стоимостью денежных ресурсов. Подставив в (10) = 0, получим

dпред. = dF / i

(13)

 

Таким образом, для товаров (услуг) длительного пользования максимальной оценкой стоимости брэнда может служить выражение (13).

ПРИМЕР:

Пусть ВАЗ производит 600 тыс. автомобилей в год.

- Ва­ловая прибыль (прибыль без налогов, фондов, амортизации) состав­ляет $1000 на один автомобиль.

- Ставка дисконтирования 6% годо­вых.

Оценим стоимость брэнда ВАЗ.

Решение:

По формуле (13) (dпред = $600тыс/ i = $10 млрд. (максимальная оценка).

По формуле (10) d= $600тыс* (1- )/( + i) = $3.4 млрд.

В последнем случае принималось, что время жизни автомобиля 10 лет —> = 1/10=10%.

Предложенная здесь методика оценки стоимости брэнда осно­вана на простом предположении:

если маркетинговые усилия по про­движению товара (услуги) положить равными нулю, то достигну­тый объем продаж начинает падать со скоростью ( 1- )`m, обеспе­чивая некоторое время соответствующие денежные потоки (при­быль).

На наш взгляд, это наиболее удобный и простой показатель для целей планирования. Конечно, не стоит его абсолютизировать как не­кий новый инструмент.

C. 126

В заключение в ознакомительных целях приведем таблицу сто­имости «мировых брэндов».

 

Компания	Страна	Стоимость брэнда, млрд. долларов (2000)	Стоимость брэнда, млрд. долларов (1999)
1.Coca-Cola	США	72,5	83,8
2. Microsoft	США	70,2	56,7
3. IBM	США	53,2	43,8
4. Intel	США	39,0	30,0
5. Nokia	Финляндия	38,5	20,7
6. General Electric	США	38,1	33,6
7. Ford	США	36,4	33,2
8. Disnev	США	33,6	32,8
9. McDonald's	США	27,9	26,2
10. AT&T	США	25,5	24,2