· Задача 1.
Проводится проверка гипотезы о равенстве цен на товар в двух регионах.
Получены следующие данные:
| Variable | Mean | Std.Dv | P-level |
| X15 | 12,1 | 1,22 | |
| X16 | 25,0 | 15,54 | 0,104 |
Можно ли считать, что средние значения цен в двух регионах равны при заданной доверительной вероятности 0,85. Ответ объяснить.
· Решение.
Так как P-level=0,104<0,15 гипотезу о равенстве средних значений цен следует отвергнуть.
· Задача 2.
Проводится проверка гипотезы о равенстве среднего дохода населения в двух регионах. Получены следующие данные:
| Variable | Mean | Std.Dv | P-level |
| X1 | 107.9146 | ||
| X2 | 248.5514 | 0,319316 |
Можно ли считать что средние доходы населения в двух регионах равны при заданной доверительной вероятности 0,8. Ответ объяснить.
· Решение.
Так как P-level=0,319316>0,2, то гипотезу о равенстве средних доходов населения в двух регионах следует принять.
· Задача 3.
Имеются следующие результаты расчётов параметров регрессионной модели:
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| Intercept | 3401.0 | 153.0 | 0.00000 | ||
| 1/V1 | -1.000 | 0.25725 | -2781000 | 7115.72 | 0.00000 |
| LN(V3) | 0.27 | 0.25725 | -8.0 | 16.72 | 0.04711 |
Какой вид имеет уравнение регрессии?
· Решение.
У=3401-2781000/V1 - 8*LN(V3)
· Задача 4.
Имеются следующие результаты расчётов параметров регрессионной модели:
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| Intercept | 23.638 | 2.07 | 0.0003 | ||
| Х**5 | 0.979 | 0.101 | 1.036 | 1.07 | 0.0006 |
Какой вид имеет уравнение регрессии?
· Решение.
У=1,036*Х5+23,638
· Задача 5.
Реляционная модель базы данных имеет следующий вид:
Товарная продукция (Вид продукции, Цена, Себестоимость, Объем продаж).
Написать SQL-запрос, позволяющий рассчитать прибыль от реализации каждого вида продукции.
· Решение.
Select [Вид продукции],(Цена-Себестоимость)*[Объем продаж]AS[Прибыль от реализации]FROM[Товарная продукция]
· Задача 6.
Реляционная модель базы данных имеет следующий вид:
Товарная продукция (Вид продукции, Цена, Себестоимость, Объем продаж).
Написать SQL-запрос, позволяющий рассчитать рентабельность продукции каждого вида.
· Решение.
Select [Вид продукции],(Цена-Себестоимость)/СебестоимостьAS[Рентабельность продукции]FROM[Товарная продукция]
· Задача 7.
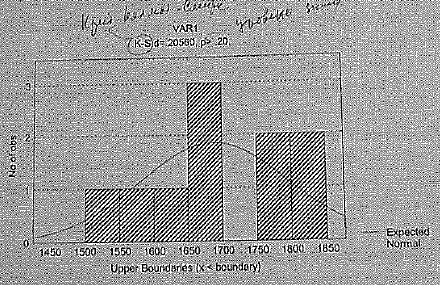
Определить, подчиняется ли случайная величина нормальному закону распределения при заданной вероятности 0,9
· Решение.
Так как расчётное значение P>0,2, то при заданной вероятности 0,9 и при уровне значимости 1-0,9=0,1, гипотезу о нормальном законе распределения следует принять.
· Задача 8.
Является ли временной ряд стационарным? Ответ объяснить.
· Решение.
Так как коэффициенты автокорреляции близки к нулю, ряд является стационарным.
· Задача 9.
Имеются следующие данные об ошибках прогноза при экспоненциальном сглаживании:
| Mean error | 0.095 |
| Mean absolute error | 0.837 |
| Sum of squares | 8.088 |
| Mean square | 1.01 |
| Mean percentage error | -1.063 |
| Mean absolute percentage error | 15.500 |
Можно ли использовать для прогнозирования эту модель? Что можно сказать о точности прогноза? Ответ объяснить.
· Решение.
Модель можно использовать, так как MPE<5%. Точность прогноза хороша, т.к. MAPE<20%
· Задача 10.
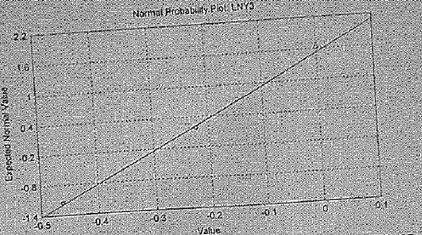
Можно ли считать распределение случайной величины нормальным? Ответ объяснить.
· Решение.
Да, так как все точки на графике близки к диагонали.
· Задача 11.
Имеются следующие результаты расчётов параметров регрессионной модели.
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| Intercept | 7,7 | 6,29 | 0,0345 | ||
| VAR1 | 0,75 | 0,105 | 0,05 | 0,006 | 0,0470 |
| VAR2 | 0,64 | 0,096 | 0,32 | 0,04 | 0,5233 |
| VAR3 | 0,68 | 0,131 | 5,3 | 1,03 | 0,0362 |
Определить, какие переменные следует включить в модель. Ответ объяснить.
· Решение.
В модель следует включить переменные, у которых P-level<0,05 то есть переменные VAR1 и VAR3
· Задача 12.
Имеются следующие результаты расчётов параметров регрессионной модели.
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| Intercept | 200,82 | 23,362 | 0,023 | ||
| VAR1 | 0,62 | 0,320 | -54,26 | 5,315 | 0,043 |
| VAR2 | 0,52 | 0,103 | 8,64 | 6,286 | 0,001 |
| VAR3 | 0,86 | 0,145 | 15,36 | 1,033 | 0,062 |
| VAR4 | 0,90 | 0,050 | -30,12 | 8,862 | 0,012 |
Определить, какие переменные следует включить в модель. Ответ объяснить.
· Решение.
В модель следует включить переменные, у которых P-level<0,05 то есть переменные VAR1 VAR2 и VAR4
· Задача 13.
Для одного и того же массива данных выполнены расчеты по двум моделям:
Модель 1.
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| Intercept | 185,531 | 224,120 | 0,454 | ||
| VAR1 | 0,408 | 0,456 | 7,430 | 8,324 | 0,423 |
Модель 2.
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| VAR1 | 0,991 | 0,065 | 13,957 | 2,548 | 0,0029 |
Какую модель следует выбрать? Какой вид имеет уравнение регрессии для выбранной модели?
· Решение.
Так как P-level<0,05 в модели 2, выбранное уравнение регрессии имеет вид:
У=13,957* VAR1
· Задача 14.
Имеются следующие результаты расчетов параметров регрессионной модели:
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| Intercept | 12,389 | 1,03 | 0,0027 | ||
| Х**2 | 0,991 | 0,065 | 0,018 | 0,01 | 0,00011 |
Какой вид имеет уравнение регрессии?
· Решение.
У=0,018*Х2+12,389
· Задача 15.
Имеются следующие результаты расчетов параметров регрессионной модели:
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| Intercept | 23,638 | 2,07 | 0,0003 | ||
| SQR-X | 0,979 | 0,101 | 1,036 | 1,07 | 0,0006 |
Какой вид имеет уравнение регрессионной модели?
· Решение.
У=1,036*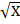 
+23,638
· Задача 16.
Имеются следующие результаты расчётов параметров регрессионной модели.
| BETA | St.Err of BETA | B | St.Err of B | P-level | |
| Intercept | 7,70 | 6,28 | 0,0345 | ||
| VAR1 | 0,75 | 0,15 | 0,05 | 0,006 | 0,0470 |
| VAR2 | 0,64 | 0,36 | 0,32 | 0,04 | 0,0423 |
| VAR3 | 0,68 | 0,34 | -5,31 | 1,03 | 0,0362 |
Какой вид имеет уравнение регрессии?
· Решение.
У=7,70+0,05* VAR1+0,32* VAR2-5,31* VAR3
· Задача 17.
Имеются следующие данные об ошибках прогноза при экспоненциальном сглаживании:
| Mean error | -1,963 |
| Mean absolute error | 2,674 |
| Sum of squares | 145,156 |
| Mean square | 10,368 |
| Mean percentage error | -27,999 |
| Mean absolute percentage error | 32,961 |
Можно ли использовать для прогнозирования эту модель? Что можно сказать о точности прогноза? Ответ объяснить.
· Решение.
Модель можно использовать, так как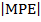 
=27,999>5%. точность прогноза следует считать неудовлетворительной, такую модель использовать нельзя.
· Задача 18.
| Номер модели | Alpha | Mean Error | Mean Abs Error | Sums of Squares | Mean Squares | Mean % Error | Mean Abs % Error |
| 0,1 | -0,88735 | 24,45301 | 19204,24 | 1600,353 | -9,84688 | 21,6203 | |
| 0,2 | -1,83242 | 26,32302 | 20497,84 | 1708,153 | -11,0994 | 23,71243 | |
| 0,3 | -2,39138 | 27,46796 | 21491,03 | 1790,919 | -11,7719 | 25,03969 | |
| 0,4 | -2,55478 | 27,71656 | 22320,12 | 1860,01 | -11,8868 | 25,4069 | |
| 0,5 | -2,45338 | 27,40177 | 23117,68 | 1926,473 | -11,6047 | 25,11176 | |
| 0,6 | -2,22704 | 27,93201 | 23969,55 | 1997,463 | -11,088 | 25,51011 | |
| 0,7 | -1,97776 | 29,21865 | 24922,67 | 2076, 889 | -10,4522 | 26,51442 | |
| 0,8 | -1,76176 | 30,2046 | 26004,12 | 2167,01 | -9,75967 | 27,09788 |
Какую модель следует выбрать для прогнозирования. Ответ объяснить. Какой вид имеет уравнение в выбранной модели?
· Решение.
Модель №1, имеющая минимальные ошибки. 
· Задача 19. 
|
|
Какой вид имеет соответствующая реляционная модель?
· Решение.
R1(O1,C1) R2(O2,C2) R3(O1,O2)
· Задача 20.
 |
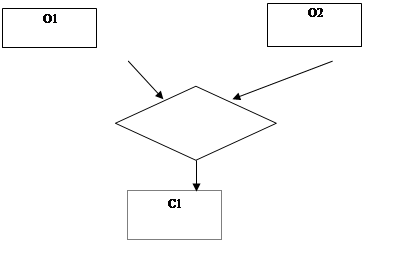Какой вид имеет соответствующая реляционная модель?
· Решение.
R1(O1,O2,C1)
Финансовый менеджмент
Математический метод
Логистика. Запасы.
Задача 1
Годовая потребность в материалах 500т.
Число рабочих дней в году 226.
Время поставки 6 дней.
Возможная задержка 1 день.
Определить max потребления за время поставки в системе с фиксированным размером заказа если известно, что ожидаемая потребность за время поставки 2 тонны.
Решение
Максимальное потребление за время поставки = (Время поставки + Задержка поставки)* расход=(6+1)*2=14т.
Задача 2
Определить в системе с фиксированным размером заказа гарант. заказ, если известно, что ожидаемое потребление составляет 80 тонн.
Максим. потребление за время поставки 100 тонн.
Решение
100-80=20т.
Задача 3
Рассчитать ожидаемое потребление за время поставки в системе управления запасами с фиксированным интервалом времени между заказами, если ожидаемое дневное потребление 100т/день, а время поставки 10 дней.
Решение
100*10=1000т.
Задача 4
В системе управления запасами с фиксир. интервалами времени между заказами определить интервал времени между заказами, если годовое потребление составляет 5000т. Число рабочих дней 226.
Оптимальный размер заказа 350 т.
Решение
Интервал времени =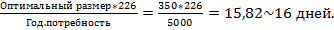 
Задача 5
В системе управления запасами с фиксированным интервалом времени определить максимально желательный запас, если интервал между заказом 11 дней.
Дневное потребление 5 тонн/день.
Гарантийный запас 10 тонн.
Решение
Макс = Гарант+ (интервал+ожидаемое дневное потребление)= 10+(11*5)=65 тонн
Задача 6
Определить долю дополнительных затрат, возникающих при доставке товара из Юго-Вост. Азии.
Решение
Транспортный тариф Т 105 долл./км.
Импортная пошлина Пи 10%
Ставка на запасы в пути Зп 1,7%
Страховые запасы Зс 0,6%
Стоимость товара в Европе (не пригод) С 108 долл.
в Юго-Вост. Азии С 80 долл.
Удельная стоимость поставки груза У 2000долл./км.
Решение
Доля дополнительных затрат Д= 
%
Д= 
Задача 7
S годовая потребность в арматуре 2000 тонн.
Цена за единицу продукции 1400 евро (I).
Стоимость хранения 25% цены.
Стоимость оформления заказа 75 евро на 1 заказ (А).
Необходимо рассчитать оптим. размер заказа по формуле Уильсона.
Решение
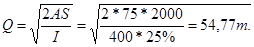
Задача 8
В фирме в течение месяца требуется техника для организации продаж. Стоимость заказа партии товара 19 евро.
Издержки хранения 10 евро.
Потребность 9 евро (П).
Определить оптимальное количество заказываемой техники.
Решение
Оптимальное количество заказываемой техники:
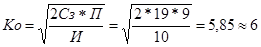шт.
Задача 9.
В течение месяца в фирме требуется техника для организации продаж.
Потребность в технике 100 шт. в месяц.
Стоимость заказа партии 10 евро.
Издержки хранения 1 товара 5 евро.
Определить оптимальное число заказов.
Решение.
Оптимальное число Ч:
заказов.
Задача 10.
В течение месяца в фирме требуется техника для организации продаж.
Потребность в технике 80 шт. в месяц.
Стоимость заказа партии 15 евро.
Издержки хранения 1 товара 9 евро.
Определить оптимальные переменные издержки.
Решение.
Чо= 
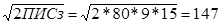евро.
Управление качеством
Решение задач
1 Анализ брака и потерь от брака
Ø Абсолютный размер брака представляет собой сумму затрат на окончательно забракованные изделия и расходов на исправление исправимого брака (Аб).
Ø Абсолютный размер потерь от брака получают вычитанием из абсолютного размера брака стоимости брака по цене использования, суммы удержаний с лиц- виновников брака и суммы взысканий с поставщиков за поставку некачественных материалов (АП.б.).
Ø Аб >АП.б.
Ø Относительные показатели размера брака и потерь от брака рассчитывают
процентным отношением абсолютного размера брака или потерь от брака соответственно к производственной себестоимости товарной продукции.
| N п/п | Показатель, ден. ед. | Предыд. год | Отчетн. год |
| Себестоимость окончательного брака Расходы по исправлению брака | 20 000 10 000 | 24 000 7 500 | |
| Абсолютный размер брака (стр.1 + стр.2) | 30 000 | 31 500 | |
| Стоимость брака по цене использования Суммы, удержанные с лиц-виновников брака Суммы, взысканные с поставщиков | 6 000 – – | 6 500 1 500 8 000 | |
| Абсолютный размер потерь от брака (стр.3 - стр.4 - стр.5 - стр.6) | 24 000 | 15 500 | |
| Валовая (товарная) продукция по производственной себестоимости | 400 000 | 420 000 | |
| Относительный размер брака (стр.3 / стр.8 * 100%) | 7,5 | 7,5 | |
| Относительный размер потерь от брака (стр.7 / стр.8 * 100%) | 6,0 | 3,7 |
2 Анализ учета затрат на качество с использованием индексов
1. Индекс затрат с учётом качества:
IЗК= 
Где 
– расход нового по качественным характеристикам сырья полученный в отчетном
периоде, нат.ед.
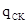–расход старого по качественным характеристикам сырья предусмотренный по
плану, нат. Ед.
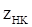– затраты (стоимость) нового сырья по отчету, ден. ед.
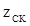– затраты (стоимость) старого сырья по плану, ден. ед.
2. Индекс, учитывающий изменение качества сырья, без изменения его стоимости:
IК=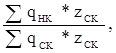 
где – расход нового по качественным характеристикам сырья, полученный в отчетном
периоде, нат.ед.
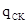–расход старого по качественным характеристикам сырья, предусмотренный по плану, нат. Ед.
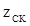– затраты (стоимость) сырья по плану, ден. ед.
3. Индекс, учитывающий изменение затрат без учета изменения качества используемого сырья:
IZ= 
где – расход нового по качественным характеристикам сырья полученный в отчетный
период, нат.ед.
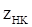– затраты (стоимость) сырья по отчету, ден. ед.
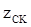– затраты (стоимость) сырья по плану, ден. ед.
Затраты на качество
Затраты на качество - это затраты, которые необходимо понести, чтобы обеспечить удовлетворенность потребителя продукцией/ услугами.
Существует несколько классификаций затрат на качество. Самый известный из них - подход Джурана -Фейгенбаума.
В соответствии с этим подходом затраты подразделяются на четыре категории:
Ø затраты на предупредительные мероприятия -это затраты на предотвращение самой возможности возникновения дефектов, т. е. затраты, направленные на снижение или полное предотвращение возможности появления дефектов или потерь;
Ø затраты на контроль - затраты на определение и подтверждение достигнутого уровня качества;
Ø внутренние потери (затраты на внутренние дефекты) — затраты, понесенные внутри организации когда запланированный уровень качества не достигнут;
Ø внешние потери (затраты на внешние дефекты) - затраты, понесенные вне организации (т. е. после того, как продукт был продан потребителю), когда запланированный уровень качества не достигнут.
Сумма всех этих затрат дает общие затраты на качество.
По данным распределения затрат на качество определить затраты на предупреждение появления дефектов.
Исходные данные, тыс. руб.:
а) информационное обеспечение
б) качество основных и вспомогательных материалов
в) технологическая подготовка производства
г) управление процессами
д) контроль и испытания в процессе производства
е) метрологическое обеспечение
ж) предупреждение появления несоответствий
з) качество упаковки, хранения и транспортировки
и) обучение и подготовка кадров
к) обслуживание
л) связь с потребителем
м) обеспечение стабильности качества и гарантии качества
н) учет, оценка и анализ затрат на обеспечение качество
Ø Решение:
Затраты на предупреждение появления дефектов = а)+в)+г)+ж)+з)+и)
По данным распределения затрат на качество, приведенным выше, определить затраты на оценку (контроль) качества.
Ø Решение:
Затраты на оценку (контроль) качества = б)+д)+е)+н)
По данным распределения затрат на качество, представленным выше, определить затраты на устранение дефектов, обнаруженных вне предприятия.
Ø Решение:
Затраты на устранение дефектов, обнаруженных вне предприятия = к)+л)+м)
Анализ сортности
На промышленном предприятии выпускается продукция двух видов, отличающихся по уровню качества сортная и несортная.
Оценить эффективность производимых на предприятии мероприятий по улучшению уровня качества (на основе анализа сортности).
Исходные данные:
| Продукция | Выпуск, тыс.т. | |
| Предыдущий год | Отчетный год | |
| Сортная | 1 952 | 2 751 |
| Не соответствующая установленным стандартам |
Решение:
1.Удельный вес сортной продукции:
В предыдущий год: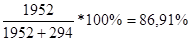 
В отчетный год: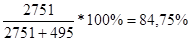 
2.Удельный вес несортной продукции:
В предыдущий год: 100–86,91=13,09%
В отчетный год: 100–84,75=15,25%
Ответ: Эффективность производимых мероприятий по улучшению качества продукции снизилась из-за увеличения доли несортной продукции на 2,16% (15,25%–13,09%)
Относительные показатели размера брака и потерь от брака рассчитывают процентным отношением абсолютного размера брака или потерь от брака соответственно к производственной себестоимости товарной продукции.
-
Индексный метод
- Индекс затрат с учетом качества в отчетном периоде по сравнению с планом:
Iзк=
Где:
qн — расход нового по качественным характеристикам сырья полученный в отчетном периоде.нат. ед.
qck -расход старого по качественным характеристикам сырья предусмотренный по плану, нат ед.
Zн- затраты (стоимость) нового сырья по отчету. ден. ед.
Zск-затраты (стоимость) старого сырья по плану, ден ед.
- Индекс, учитывающии изменение качества сырья, без изменения его стоимости в отчетном периоде по сравнению с планом:
Iк=
- Индекс, учитывающий изменение затрат на продукцию, без учета изменения качества используемого сырья:
Iz=
3. 3атраты на качество
Затраты на качество - это затраты которые необходимо понести, чтобы обеспечить удовлетворенность потребителя продукцией/ услугами.
Существует несколько классификаций затрат на качество. Самый известный из них - подход Джурана -Фейгенбаума.
В соответствии с этим подходом затраты подразделяются на четыре категории:
- затраты на предупредительные мероприятия -это затраты на предотвращение самой возможности возникновения дефектов, т. е. направленные на снижение или полное предотвращение возможности появления дефектов или потерь;
- затраты на контроль - затраты на определеиие и подтверждение достигнутого уровня качества
- внутренние потери (затраты на внутренние дефекты) — затраты, понесенные внутри организации когда запланированный уровень качества не достигнут
- внешние потери (затраты на внешние дефекты) - затраты, понесенные вне организации (т. е. после того, как продукт был продан потребителю), когда запланированный уровень качества не достигнут.