Задача №1
Расставить знаки корректировок («+» или «-» или «0») при оценке объекта оценки (квартиры) сравнительным подходом:
а) объект оценки находится на 5 этаже 12-ти этажного дома. Объект сравнения № 1 на 10 этаже, объект сравнения № 2 на 1 этаже аналогичного дома;
б) объект оценки находится на расстоянии 10 минут ходьбы пешком от станции метро «М». Объект сравнения № 3 - на расстоянии 15 минут, а объект сравнения № 4 на расстоянии 6 минут ходьбы пешком от станции метро «М»;
в) объект оценки приватизирован. Объект сравнения № 5 является муниципальной собственностью, а объект № 6 получен в наследство, которое оформлено на собственника.
Решение.
а) № 1 - «+», № 2 - «+».
б) № 3 - «+», № 4 - «-».
в) № 5 - «+», № 6 - «0».
Задача № 2
Расставить знаки корректировок («+» или «-» или «0») при оценке объекта оценки (квартиры) сравнительным подходом:
а) объект оценки не приватизирован. Объект сравнения № 1 приватизирован, объект сравнения № 2 куплен в кредит и оформлен в виде залога за полученный кредит;
б) дата оценки объекта оценки 21 декабря текущего года. Инфляция строительной продукции составляет более 1 % в месяц. Данные по объекту сравнения № 3 используются по состоянию на 5 сентября текущего года;
в) на дату оценки на объекте оценки проведен ремонт. Объект сравнения № 4 находится в эксплуатации без ремонта около 3 лет, а на объекте сравнения № 5 за 3 месяца до даты оценки проведен ремонт с повышенным качеством и он после ремонта не эксплуатировался.
Решение.
а) № 1 - «-», № 2 - «-».
б) № 3 - «+».
в) № 4 - «+», № 5 - «-».
Задача № 3
Определить стоимость земельного участка, если известно, что стоимость земельного участка с расположенными на нем объектами недвижимости составляет 1200 тысяч рублей, а чистый операционный доход, получаемый от использования объектов недвижимости составляет 200 тысяч рублей в год. Известны рыночные коэффициенты капитализации для недвижимости - 0,25 и для земельных участков - 0,10.
Решение.
С = Сз + Сн
Сз = С - ЧОДн/Rн
Сз = 1200000 - 200000/0,25 = 1200000 - 800000 = 400000 руб.
Задача № 4
Определить стоимость собственных и заемных средств по проекту, если известно, что чистый операционный доход по проекту равен 300 тысяч рублей в год, собственные средства составляют 1 миллион рублей, рыночные коэффициенты капитализации равны: 0,20 - для собственных средств и 0,25 - для заемных средств.
Решение.
С = С соб + С заем = ЧОДсоб/Ксоб + ЧОДзаем/Кзаем;
ЧОДсоб + ЧОДзаем =300000 руб.
ЧОДсоб / 0,2 = 1000000 руб.
ЧОДсоб = 200000 руб.
ЧОДзаем = 300000 - 200000 = 100000 руб.
С = 1000000 + 100000/0,25 = 1000000 + 400000 = 1400000 руб.
Задача № 5
Рыночная стоимость объекта оценки, рассчитанная доходным подходом (методом построения) составила 5 миллионов рублей при суммарной норме дисконтирования 0,185. На сколько процентов изменится рыночная стоимость объекта оценки, если в качестве безрисковой ставки будет использован процент по государственным ценным бумагам России (который меньше на 1,5 %) вместо процента по депозитам Сбербанка России. Все другие условия, показатели и риски остаются неизменными.
Решение:
С0 = ЧОД0 / N0; С1 = ЧОД0 / (N0 - D N);
(С1 / С0 - 1) ´ 100 = (N0 / (N0 - D N) - 1) ´ 100
(0,185 / 0,170 - 1) ´ 100 @ 8,82 %
Пояснение:
N0 – НОРМА дисконтирования;
ЧОД – Чистый операционный доход.
0,170 = 0,185 – 1,5/100 (1,5%)
Задача № 6
На сколько процентов различается рыночная стоимость аналогичных объектов оценки в регионах «А» и «Б», рассчитанная доходным подходом (методом построения) при следующих условиях:
- рыночная стоимость объекта оценки в регионе «А» равна 10 млн. рублей при суммарной норме дисконтирования 15 %;
- годовая инфляция, учтенная при расчете суммарной нормы дисконтирования в регионе «Б» больше, чем в регионе «А» на 3 %.
Все другие условия, показатели и риски одинаковы.
Решение.
Са= ЧОДа / Nа ; Сб= ЧОДб / Nб ;
ЧОДа = ЧОДб
Nб = Nа + 0,03
Сб /Са - 1 = Nа / Nб - 1 = Nа / (Nа + 0,03) - 1;
0,15 / (0,15 + 0,03) - 1 = 0,15 / 0,18 - 1 @ 0,167 или 16,7 %
Задача № 7
Определить стоимость объектов недвижимости, если известно, что стоимость земельного участка с расположенными на нем объектами недвижимости составляет 3 миллиона рублей, а чистый операционный доход, получаемый от использования земельного участка составляет 98 тысяч рублей. Известны рыночные коэффициенты капитализации для недвижимости - 0,15 и для земельных участков - 0,07.
Решение.
С = Сз + Сн
Сн = С - ЧОДз/Rз
Сн = 3000000 - 98000/0,07 = 3000000 - 1400000 = 1600000 руб.
Задача № 8
\Определить стоимость собственных и заемных средств по проекту, если известно, что чистый операционный доход по проекту равен 100 тысяч рублей в год, заемные средства составляют 0,5 млн. рублей, рыночные коэффициенты капитализации равны: 0,14 - для заемных средств и 0,10 - для собственных.
Решение:
С = С соб + С заем = ЧОДсоб/Ксоб + ЧОДзаем/Кзаем;
ЧОДсоб + ЧОДзаем = 100000 руб.
ЧОДзаем / 0,14 = 500000 руб.
ЧОДзаем = 70000 руб.
ЧОДсоб = 100000 - 70000 = 30000 руб.
С = 30000/0,10 + 500000 = 300000 + 500000 = 800000 руб.
Задача №9
Распределите исходные данные по объекту сравнения по элементам корректировки.
Объект сравнения № 1, приватизированный в 1992 г., продан с известной ценой продажи за 4 месяца до даты оценки объекта оценки со следующими характеристиками (отличными от объекта оценки): капитальный ремонт произведен в 1998 году с полной заменой электрических точек (выключателей, розеток и т.п.) и электроплиты, сантехнического оборудования, пола, дверных и оконных проемов, установкой подвесных потолков (высота до потолка уменьшилась до 2,95 м).
Решение.
1. Права собственности - затраты на приватизацию.
2. Условия рынка - инфляция строительной продукции за 4 месяца до даты оценки.
3. Физические характеристики - высота до потолка.
4. Экономические характеристики - затраты на капитальный ремонт.
5. Компоненты стоимости, не связанные с недвижимостью - электроплита, подвесные потолки.
Задача №10
Распределите исходные данные по объекту сравнения по элементам корректировки.
Объект сравнения № 2 используемый в качестве офиса продан с рассрочкой оплаты за 10 дней до даты оценки объекта оценки (квартиры) со следующими характеристиками, отличными от объекта оценки: объект сравнения № 2 находится дальше от центра города, общая площадь больше в полтора раза, отсутствует ванная и душ, имеется компьютерная разводка, встроенные шкафы.
Решение.
1. Условия финансирования - рассрочка оплаты.
2. Местоположение - удаленность от центра.
3. Физические характеристики - общая площадь, ванная и душ.
4. Использование - офисные помещения.
5. Компоненты стоимости, не связанные с недвижимостью - компьютерная разводка и встроенные шкафы.
11.При какой форме здания…
квадрат
12. Какие пункты взодят в операционные расходы
постоянные расходы +
переменные расходы +
расходы на замещение +
коммуальные
13. По каким критериям производится анализ наибольшей эффективности
законодательное разрешение +
физич. Осущ +
экономическая целесообразность +
min экологическое последствие
max продуктивность +
14. При оценке затратным подходом есть данные по удельной стоимости строительства 1м2 жилой недвижимости на июнь 2010 года. Дата оценки январь 2011 г. Какой индекс исаользуется при оценке объекта
индекс удорожания стоимости за 2-е полугодие 2010 г. +
15. Какие мероприятия приведут к изменению экономического местоположения (временные стоимостные связи) объекта жилой недвижимости?
1) рядом расположенная промзона ликвидирована +
2) на месте промзоны построили складской терминал +
3) поблизости построили платную автодорогу +
4) рядом закрылся магазин повседневных продуктов питания +
16. Какие виды износа учитываются при оценке недвижимости затратным подходом:
1) физический +
2) функциональный +
3) моральный
4) внешний +
5) эргономический
17. Отметьте, где наиболее применим затратный подход при оценке недвижимости:
1) при оценке жилой недвижимости
2) при оценке уникальных объектов недвижимости
3) при высокой активности на рынке недвижимости
4) при низкой активности на рынке недвижимости +
5) при страховании объекта недвижимости +
6) при купле-продаже объекта недвижимости
7) при переоценке основных фондов +
18. Отметьте, где наиболее применим сравнительный подход при оценке недвижимости:
1) при оценке некоммерческой недвижимости +
2) при оценке уникальных производственных помещений
3) при высокой активности на рынке недвижимости +
4) при низкой активности на рынке недвижимости
5) при купле-продаже объекта недвижимости +
6) при налогообложении объекта недвижимости
19. Какие показатели необходимо обосновать и рассчитать для применения метода дисконтированных денежных потоков в оценке недвижимости при её использовании в текущем положении?
1) срок окупаемости
2) срок проекта +
3) прогноз денежных потоков +
4) норма дисконтирования +
5) коэффициент капитализации
20. Какие позиции используются при оценке недвижимости?
1) отражающие точку зрения пользователя +
2) отражающие точку зрения рынка +
3) отражающие точку зрения оценщика
4) отражающие взаимоотношения компонентов собственности +
5) отражающие наилучшее и наиболее эффективное использование +
6) отражающие запросы продавца
Финансы и кредит
Задача № 1
Определить величину денежных агрегатов М0, М1, М2, М3 на основании следующих данных (в млн. ден. ед.):
- наличные денежные средства в банках 500
- срочные вклады населения в Сберегательном банке 1630
- депозитные сертификаты 645
- расчётные, текущие счета юридических лиц 448
- вклады населения до востребования 300
- наличные денежные средства в обращении 170.
Решение:
М0 = наличные денежные средства в обращении;
М1= М0+расчётные и текущие счета юридических лиц+вклады населения до востребования;
М2=М1+срочные вклады населения в сберегательном банке;
М3= М2+депозитные сертификаты и облигации госзайма.
Ответ: М0=170, М1=918, М2=2548, М3=3193 млн. ден. ед.
Задача № 2
Дефлятор ВНП составляет 3,6. Номинальный ВНП 4 трлн. руб. Определить реальный ВНП.
Решение:
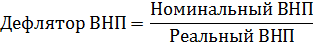
Ответ: 1,11 трлн. руб.
Задача № 3
Первоначальная сумма Р = 7000 руб. помещена в банк на срок n = 2 года под процентную ставку i = 15% годовых. Определить будущую сумму, при условии, что начисление процентов осуществляется по схеме простых процентов.
Решение:
FV=P*(1+n*i)
Ответ: 9100 руб.
Задача № 4
Первоначальная сумма Р = 6000 руб., наращенная сумма S = 7200 руб., процентная ставка i = 10% годовых (проценты простые). Определить период начисления процентов (n).
Решение:
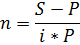
Ответ: 2 года
Задача № 5
Наращенная сумма S = 20000 руб., период начисления процентов n = 1,5 года, простая процентная ставка i = 17% годовых. Определить первоначальную сумму (P).
Решение:
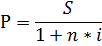
Ответ: 15936,25 руб.
Задача № 6
Первоначальная сумма Р = 24000 руб. В первой половине года применялась простая процентная ставка i1 = 12% годовых, во второй половине года применялась простая процентная ставка i2 = 15% годовых. Определить наращенную сумму (S).
Решение:
)
S=P*(1+n1*i1+n2*i2)
Ответ: 27240 руб.
Задача № 7
Кредит на сумму 15000 руб. выдаётся на полгода по простой учётной ставке 12% годовых. Определить, какую сумму получит заёмщик.
Решение:
P=S*(1-n*d)
Ответ: 14100 руб.
Задача № 8
Вексель на сумму 35000 руб. с датой погашения 27 ноября 2010 года был учтён банком 11 августа 2010 года по простой учётной ставке 13% годовых. Продолжительность года составляет 365 дней. Определить, какая сумма была выплачена банком.
Решение:
P=S*(1-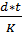 
).
t= 21(август)+30 (сентябрь)+31 (октябрь)+27 (ноябрь) -1=108 дней
Р=35000*(1-0,13*108/365)=33653,70
Ответ: 33653,70 руб.
Задача № 9
Первоначальная сумма Р = 37000 руб. помещена в банк на срок n = 2 года под i = 15% годовых (проценты сложные). Определить наращенную сумму.
Решение:
S=P*(1+i)n
Ответ: 48932,5 руб.
Задача № 10
Наращенная сумма S = 41000 руб., период начисления процентов составляет 2 года, сложная процентная ставка = 15% годовых. Определить первоначальную сумму.
Решение:
Р = 
Ответ: 31001,89 руб.
Задача № 11
Первоначальная сумма P = 24000 руб., период начисления процентов составил 5 лет, причём в первые три года применялась сложная процентная ставка равная 12% годовых, а в оставшиеся два года применялась сложная процентная ставка равная 15% годовых. Определить наращенную сумму.
Решение:
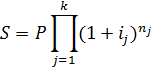
S=P*(1+i1)n1*(1+i2)n2
Ответ: 65458,27 руб.
Задача № 12
Первоначальная сумма составляет 14000 руб., период начисления процентов равен двум годам, сложная номинальная процентная ставка составляет 12% годовых. Проценты начисляются ежеквартально. Определить наращенную сумму.
Решение:
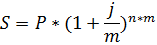
Ответ: 17734,78 руб.
Задача № 13
Первоначальная сумма P = 7000 руб., период начисления n = 4 года, сложная учётная ставка составляет 13% годовых. Определить наращенную сумму.
Решение:
Ответ: 12218,59 руб.
Задача № 14
Каждый месяц цены растут на 2%. Определить, каков ожидаемый индекс инфляции за год.
Решение:
Индекс инфляции (Iигод) = (1+рост цены)n, где n = 12 мес.
Ответ: т.е. цены за год вырастут в 1,27 раза или на 27%
Задача № 15
Уровень инфляции в марте составил 3%, в апреле – 5%, в мае – 3%. Определить индекс инфляции за рассматриваемый период.
Решение: Iигод=(1+αмарт)*(1+αапрель)*(1+αмай)
Ответ: 11,4%
Задача № 16
Период начисления (n) составляет 6 месяцев (0,5 года), ожидаемый ежемесячный уровень инфляции 1,5%. Под какую простую ставку ссудных процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность i = 6% годовых (проценты простые).
Решение:
Iигод = (1+ α)n =(1+0,015)6 = 1,0934, т.е. уровень инфляции (α) за рассматриваемый период составил 0,0934, тогда
Ставка ссудных процентов =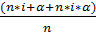 
= 
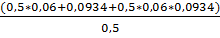= 0,2524, т.е. 25,24% годовых
Ответ: 25,24% годовых.
Задача № 17
Первоначальная сумма положена в банк на срок январь-июнь под простую ставку ссудных процентов iα=25% годовых. Уровень инфляции в январе составил 0,5%, в феврале – 2%, в марте – 1%, в апреле – 0,5%, в мае – 3%, в июне – 1%. Определить, какова реальная доходность в виде годовой простой ставки ссудных процентов.
Решение:
n = 6 месяцев = 0,5 года.
Iигод =(1+0,005)*(1+0,02)*(1+0,01)*(1+0,005)*(1+0,03)*(1+0,01)=1,0825, т.е. уровень инфляции за рассматриваемый период α =0,0825. Тогда реальная доходность в виде годовой простой ставки ссудных процентов
i = 
Ответ: 7,9% годовых.
Задача №18
Период начисления составляет 2 года, ожидаемый ежегодный уровень инфляции 12%. Определить, под какую ставку ссудных процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность i = 6% годовых (проценты сложные).
Решение:
Iи=(1+iα)n =(1+0,12)2=1,2544, т.е. α=0,2544
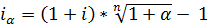=(1+0,06)* 
- 1=0,1872
Ответ: 0,1872 или 18,72% годовых.
Задача № 19
Первоначальная сумма внесена на счёт в банке на срок 2 года под сложную ставку ссудных процентов iα = 15% годовых. Уровень инфляции за первый год составил 12%, за второй год – 14%. Определить, какова реальная доходность в виде сложной годовой ставки ссудных процентов.
Решение:
Iи = (1+0,12)*(1+0,14)=1,2768, т.е. уровень инфляции α за рассматриваемый период составил 0,2768. Следовательно, реальная доходность в виде сложной годовой процентной ставки ссудных процентов будет равна:
i= 
= 
- 1=0,0177 или 1,77% годовых.
Ответ: 1,77% годовых.
Задача № 20
Определить, какой вариант инвестирования первоначальной суммы на срок 0,5 года лучше: под простую процентную ставку 18% годовых или под простую учётную ставку 16% годовых.
Решение:
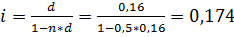(или 17,4% годовых), т.к. 17,4% ˂18%, то лучше вариант с постой процентной ставкой.
Ответ: лучше вариант с простой процентной ставкой.
Задача № 21
Определить, какой вариант инвестирования первоначальной суммы на срок 2 года лучше: под простую процентную ставку 17% годовых или под сложную процентную ставку 15,5% годовых.
Решение:
i= 
=((1+0,155)2-1)/2= 0,167 или 16,7% годовых, т.к. 16,7%˂17%, то лучше вариант с простой процентной ставкой.
Ответ: лучше вариант с простой процентной ставкой.
Задача № 22
Определить, какой вариант инвестирования первоначальной суммы на срок 2 года лучше: под простую процентную ставку 19% годовых или под номинальную сложную процентную ставку 14% годовых с ежемесячным начислением.
Решение:
=((1+0,14/12)2*12-1)/2=0,1605 или 16,5% годовых, т.к. 16,5%˂19%, то лучше вариант с простой процентной ставкой.
Ответ: лучше вариант с простой процентной ставкой.
Задача № 23
Найти эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке 12% годовых с ежемесячным начислением.
Решение:
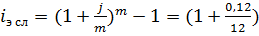12 -1=0,1268 или 12,68% годовых
Ответ: 12,68% годовых
Задача № 24
Найти годовую номинальную сложную процентную ставку (проценты начисляются каждые полгода), эквивалентную сложной процентной ставке 20% годовых.
Решение:
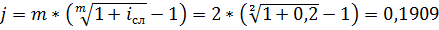, т.е. 19,09% годовых.
Ответ: 19,09% годовых
Задача № 25
Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Найти будущую сумму ренты постнумерандо.
Решение:
= 4127,52 руб.
Ответ: 4127,52 руб.
Задача № 26
Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Найти будущую сумму ренты пренумерандо.
Решение:
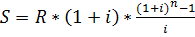= 4705,37 руб.
Ответ: 4705,37 руб.
Задача № 27
Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Определить современную стоимость простой ренты постнумерандо.
Решение:
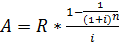= 2785,96 руб.
Ответ: 2785,96 руб.
Задача № 28
Определить размер ежегодных платежей в конце года по сложной процентной ставке 14% годовых для накопления через 4 года суммы 70000 руб. (простая рента постнумерандо).
Решение:
=14224,33 руб.
Ответ: 14224,33 руб.
Задача № 29
Определить размер ежегодных платежей в начале года по сложной процентной ставке 14% годовых для накопления через 4 года суммы 70000 руб. (простая рента пренумерандо).
Решение:
=12477,49 руб.
Ответ: 12477,49 руб.
Задача № 30
Взят кредит на сумму 60000 руб. сроком на 4 года под 15% годовых. Определить размер ежегодных погасительных платежей в конце года.
Решение:
= 21015,92 руб.
Ответ: 21015,92 руб.
Задача № 31
Взят кредит на сумму 60000 руб. сроком на 4 года под 15% годовых. Определить размер ежегодных погасительных платежей в начале года.
Решение:
= 18274,71 руб.
Ответ: 18274,71руб.
Задача № 32
Найти наращенную сумму общей ренты сроком (n) 2 года с выплатами (W) по 7000 руб. в конце каждого квартала (p) и начислением процентов по ставке (i) 11% годовых ежемесячно (m).
Решение:
7000*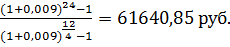 
Ответ: 61640,85 руб.
Задача № 33
Выдан кредит на сумму 50000 руб. на 3 года по ставке 16% годовых ежеквартально. Определить размер полугодовых платежей.
Решение:
Здесь р = 2, m = 4, i =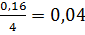 
, n = 3*m = 3*4 = 12.
= 
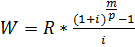=5327,61* 
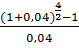=10868,32 руб.
Ответ: 10868,32 руб.
Задача № 34
Найти современную стоимость общей бессрочной ренты с выплатами по 9000 руб. в начале каждого полугодия и процентной ставкой 12% годовых ежеквартально.
Решение:
Здесь р = 2, m = 4, i = 
.
= 
Тогда А=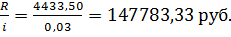 
Ответ: 147783,33 руб.
Задача № 35
10 августа заёмщик обратился за получением ломбардного кредита и предоставил в залог ценности на сумму 90000 руб. Сумма ломбардного кредита составила 75% от стоимости залога, процентная ставка 14% годовых. Определить величину кредита.
Решение:
Ломбардный кредит обычно выдаётся на 3 месяца, используется французская практика (продолжительность года К=360 дней, учитывается точное количество дней в месяце). Следовательно, кредит предоставлен на 3 месяца (10 августа – 10 ноября), его срок составляет t = 22 дня (август) + 30 дней (сентябрь) + 31 день (октябрь) + 10 дней (ноябрь) – 1= 92 дня.
Определяем сумму ломбардного кредита Р = 90000 руб.*0,75 =67500 руб.
Далее определяем проценты I =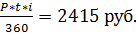 
Заёмщик получит сумму в размере = 67500 – 2415 = 65085 руб.
Ответ: 65085 руб.
Задача № 36
Заёмщик должен одному кредитору следующие суммы P1 = 7000 руб. (срок погашения 17 июля, процентная ставка i1=9% годовых), Р2=9000 руб. (срок погашения 23 августа, процентная ставка i2 = 10% годовых), Р3 = 10000 руб. (срок погашения 14 сентября, процентная ставка i3= 12% годовых). Определить когда лучше выплатить весь долг сразу (процентная ставка is=11% годовых), чтобы при этом не понесли ущерба ни кредитор, ни заёмщик.
Решение:
Примем дату первого погашения – 17 июля – за нулевой момент времени. Тогда t1=0, t2 (17 июля – 23 августа) = 38 дней, t3 (17 июля – 14 сентября) = 60 дней.
Средний срок погашения ссуды (ts) = 
= 
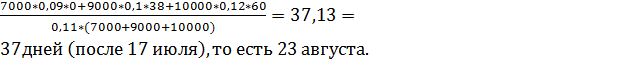
Ответ: 23 августа.
Задача № 37
Схема налога на проценты: 3% с части дохода от 0 до 5000 руб.; 5% с части дохода от 5000 до 15000 руб.; 8% с части дохода от 15000 до 30000 руб.; 12% с части дохода от 30000 до 50000 руб. и 20% с части дохода свыше 50000 руб. Начислены проценты в размере 56000 руб. Найти среднюю и предельную ставки налога.
Решение:
Разобьём сумма начисленных процентов (56 000 руб.) на части, соответствующие предельным ставкам налога: 56000 = 5000+10000+15000+20000+6000. С каждой части удерживаем соответствующий налог: 5000*0,03+10000*0,05+15000*0,08+20000*0,12+6000*0,2=5450 руб.
Средняя ставка налога 5450/56000*100%=9,73%.
Так как величина начисленных процентов составляет 56000 руб., то предельная ставка налога будет равна 20%.
Ответ: средняя ставка составляет 9,73%; предельная ставка налога 20%.
Задача № 38
Первоначальная сумма составляет 7000 руб., период начисления 0,25 года, простая процентная ставка – 14% годовых, ставка налога на проценты – 12%. Определить наращенную сумму.
Решение:
S=P*(1+i*n*(1-q)) = 7000*(1+0,14*0,25*(1-0,12))=7215,6 руб.
Ответ: 7215,6 руб.
Задача № 39
Первоначальная сумма составляет 7000 руб. период начисления 0,5 года, простая учётная ставка 15% годовых, ставка налога на проценты 11%. Найти наращенную сумму.
Решение:
= 
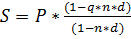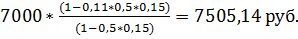
Ответ: 7505,14 руб.
Задача № 40
Первоначальная сумма составляет 12000 руб., период начисления 2 года, сложная процентная ставка 14% годовых, ставка налога на проценты 10%. Найти наращенную сумму.
Решение:
S=P*((1-q)*(1+i)n+q) = 12000*((1-0,1)*(1+0,14)2+0,1)=15235,68 руб.
Ответ: 15235,68 руб.
Задача № 41
При выдаче кредита на 0,25 года по простой процентной ставке 14% годовых удерживаются комиссионные (h) в размере 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки простых процентов (iэ).
Решение:
iэ=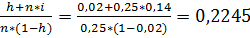 
, т.е. 22,45% годовых.
Ответ: 22,45% годовых
Задача № 42
При выдаче кредита на 2 года по простой процентной ставке 18% годовых, удерживаются комиссионные 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки сложных процентов.
Решение:
iэ= 
= 
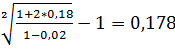, т.е. 17,8% годовых.
Ответ: 17,8% годовых.
Задача № 43
При выдаче кредита на 2 года по сложной процентной ставке 14% годовых удерживаются комиссионные 2% суммы ссуды. Определить доходность этой операции в виде эффективной ставки сложных процентов.
Решение:
iэ=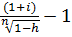 
= 
=0,1516, т.е. 15,16% годовых.
Ответ: 15,16% годовых.
Задача № 44
В апреле объём продаж составил 250000 руб. Себестоимость проданной продукции равна 110000 руб., а расходы (арендная плата, зарплата и т.д.) – 40000 руб. Определить валовую и чистую прибыль.
Решение:
Валовая прибыль = Объём продаж – Себестоимость проданной продукции = 250000 – 110000 = 140 000 руб.
Чистая прибыль = Валовая прибыль – Расходы = 140000 – 40000 = 100000 руб.
Ответ: 140000 руб., 100000 руб.
Задача № 45
На конец финансового года внеоборотные активы предприятия составила 120000 руб., оборотные активы – 50000 руб., краткосрочные обязательства – 60000 руб. В течение отчётного финансового года объём продаж составил 350000 руб. Определить коэффициент оборачиваемости чистых активов.
Решение:
Коэффициент оборачиваемости чистых активов = Выручка от продаж: Суммарные чистые активы;
Суммарные чистые активы = Внеоборотные активы + Оборотные активы – Краткосрочные обязательства.
Коэффициент оборачиваемости чистых активов = 3,18, т.е. за 1 год чистые активы предприятия совершают 3,18 оборота.
Ответ: 3,18 оборота.
Задача № 46
На конец финансового года запасы предприятия составили 35000 руб., дебиторская задолженность – 13000 руб., кассовая наличность – 4000 руб., краткосрочные обязательства – 58000 руб. Определить коэффициент текущей ликвидности.
Решение:
КТЛ = Оборотные активы: Краткосрочные обязательства,
КТЛ = 0,90, т.е. на 1 рубль краткосрочных обязательств приходится 0,90 руб. оборотных активов. Рекомендуемое значение КТЛ ≥ 2
Ответ: 0,90
Задача № 47
На конец финансового года запасы предприятия составили 35000 руб., дебиторская задолженность – 23000 руб., кассовая наличность – 34000 руб., краткосрочные обязательства – 68000 руб. Определить коэффициент срочной ликвидности.
Решение:
Коэффициент срочной ликвидности = (Оборотные активы – Запасы): Краткосрочные обязательства.
Коэффициент срочной ликвидности = 0,84, т.е. на дату составления бухгалтерского баланса только 84% краткосрочных обязательств может быть погашено в короткий срок за счет оборотных активов, если запасы не представляется возможным перевести в наличные денежные средства. Рекомендуемое значение ˃1, Обычное значение: 0,7-0,8.
Ответ: 0,84.
Задача № 48
На конец финансового года средние запасы предприятия составили 35000 руб., себестоимость проданной продукции – 105000 руб. Определить коэффициент оборачиваемости запасов.
Решение:
Коэффициент оборачиваемости запасов = Себестоимость проданной продукции: Средняя величина запасов
Коэффициент оборачиваемости запасов = 3.
Ответ: 3.
Задача № 49
Средняя величина дебиторской задолженности предприятия составила 35000 руб., объём продаж в кредит – 190000 руб. Определить период оборачиваемости дебиторской задолженности. Продолжительность года составляет 360 дней.
Решение:
Период оборачиваемости дебиторской задолженности = (360* Средняя величина дебиторской задолженности): Выручка от продаж (объём продаж в кредит).
Период оборачиваемости дебиторской задолженности = 66 дней, т.е. в среднем проходит 66 дней с момента отгрузки продукции до поступления денежных средств на счета предприятия.
Ответ: 66 дней
Задача № 50
Средняя величина кредиторской задолженности предприятия составила 45000 руб. Объём закупок в кредит – 240000 руб. Определить период оборачиваемости кредиторской задолженности. Продолжительность года составляет 360 дней.
Решение:
Период оборачиваемости кредиторской задолженности = (Средняя величина кредиторской задолженности*360): Производственную себестоимость (объём закупок в кредит).
Период оборачиваемости кредиторской задолженности = 67,5 дней, т.е. средний срок погашения кредиторской задолженности составляет 68 дней.
Ответ: 67,5 дней.
Задача № 51
В марте закуплены для реализации 600 единиц продукции по цене 15 руб./ед. В апреле – июле проданы 450 единиц продукции по цене 25 руб./ед. В начале августа непроданная продукция была уценена до 15 руб./ ед. и по этой цене проданы 50 единиц продукции. Определить процент скидки.
Решение:
Процент скидки = (денежная сумма скидки: суммарный объём продаж)*100%.
Денежная сумма скидки = 50*(25-15) = 500 руб.
Суммарный объём продаж = 450*25+50*15 = 12000 руб.
Процент скидки = (500/12000 руб.) *100% = 4,17%.
Ответ: 4,17%
Задача № 52
Определить коэффициент рентабельности чистых активов на основании следующих данных: чистая прибыль составляет 40000 руб., внеоборотные активы предприятия – 120000 руб., оборотные активы – 50000 руб., краткосрочные обязательства – 60000 руб.
Решение:
Коэффициент рентабельности чистых активов = (Чистая прибыль: Суммарные чистые активы)* 100% = (40000: 110000)*100% = 36,36%.
Ответ: 36,36%
Задача № 53
Определить текущую рыночную стоимость облигации при следующих данных: текущая рыночная процентная ставка составляет 18%, номинальная стоимость облигации – 5000 руб., купонная процентная ставка – 15%, оставшийся срок до погашения облигации составляет 3 года.
Решение:
Облигацию следует рассматривать как простую ренту постнумерандо, состоящую из выплат купонных процентов и возмещения номинальной стоимости облигации. Следовательно, текущая стоимость облигации равна современной стоимости этой ренты.
Величина купонных платежей (R) = k*P = 0,15*5000 = 750 руб.
Текущая рыночная стоимость облигации (An) = R* 
=750* 
+ 
Ответ: 4673,86 руб.
Задача № 54
Облигация номинальной стоимостью - 1000 руб. с купонной процентной ставкой – 15% была приобретена в начале года за 700 руб. После получения купонного платежа в конце года облигация была продана за 750 руб. Определить норму прибыли за год.
Решение:
Норма прибыли = (купонный платёж + цена облигации в конце периода – цена облигации в начале периода): цена облигации в начале периода
Величина купонных платежей = 0,15*1000 = 150 руб.
Норма прибыли облигации за год = (150+750 – 700): 700 = 0,2857 или 28,57% годовых.
Ответ: 28,57% годовых.
Задача № 55
Облигация номинальной стоимостью – 1000 руб. с купонной процентной ставкой – 15% и сроком погашения – 10 лет была куплена за 800 руб. Определить доходность облигации методом средних.
Решение:
Величина купонных платежей = 0,15*1000 = 150 руб.
Общая сумма выплат = 10 лет*150 руб. + 1000 руб. = 2500 руб.
Общая прибыль = 2500 – 800 = 1700 руб.
Средняя прибыль за один период = 1700/10 = 170 руб.
Средняя стоимость облигации = (1000+800)/2 = 900 руб.
Доходность облигации = 170/900 = 0,1889 или 18,89%.
Ответ: 18,89%
Задача № 56
Номинальная стоимость облигации составляет 5000 руб., купонная процентная ставка – 15%, оставшийся срок до погашения облигации – 3 года, текущая рыночная процентная ставка составляет 12%. Определить дюрацию облигации.
Решение:
Дюрация облигации – средний срок возврата капитала для инвестора, вкладывающего средства в приобретение этой облигации.
Величина купонных платежей (R) = 0,15*5000 = 750 руб.
Поток платежей по облигации будет иметь следующий вид: S1=S2=R=750, S3=R+P = 750+5000 = 5750 руб.
Дюрация (D) =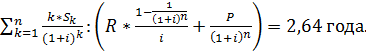 
Ответ: 2,64 года.
Задача № 57
Определить коэффициент эластичности настоящей стоимости будущих доходов по ставке процента на основании следующих данных: дюрация составляет 2,634, текущая рыночная процентная ставка – 12%.
Решение:
Коэффициент эластичности показывает, на сколько процентов изменится стоимость потока фиксированных платежей по облигации при изменении ставки процента на рынке капитала на 1%.
Эластичность = D* 
,282 или 28,2%
Ответ: 0,282 или 28,2%.
Задача № 58
По обращающимся привилегированным акциям выплачиваются ежегодные дивиденды в размере 50 руб. Цена акции составляет 500 руб. Определить доходность акции.
Решение:
Доходность акции = дивиденд/цена (курс) акции = 50/500 = 0,1 или 10%.
Ответ: 10%.
Задача № 59
Рыночная цена акции в настоящий момент составляет 110 руб. Ожидаемая цена акции в конце текущего года составит 120 руб. ожидаемый дивиденд в текущем году будет равен 5 руб. Определить ожидаемую дивидендную доходность, ожидаемую доходность за счёт изменения цены акции и ожидаемую доходность по акции в текущем году.
Решение:
Ожидаемая дивидендная доходность в текущем году = 5/110 = 0,05 или 5%.
Ожидаемая доходность за счёт изменения цены акции = (120-110)/110 = 0,091 или 9,1%.
Ожидаем