При моделировании детерминированных факторных систем необходимо выполнять ряд требований:
ü факторы, которые включаются в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть абстрактными придуманными величинами или явлениями;
ü факторы, входящие в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми явлениями;
ü все показатели модели должны быть количественно измеримыми, т.е. иметь единицу измерения и необходимую информационную обеспеченность;
ü в модели должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияний отдельных факторов должна быть равна общему приросту результативного показателя.
В анализе выделяют следующие типы факторных моделей[13]:
1. Аддитивные модели – используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей
. (2.1)
2. Мультипликативные модели – применяются, когда результативный показатель представляет собой произведение факторов
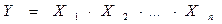. (2.2)
3. Кратные модели
. (2.3)
Смешанные модели
. (2.4)
Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного разложения факторов исходной системы на факторы-сомножители
ВП=Ч∙ГВ=Ч∙Д∙ДВ=Ч∙Д∙П∙ЧВ. (2.5)
Степень детализации зависит от цели исследования.
К кратным моделям применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения.
Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму показателей.
|
|
Например: себестоимость единицы продукции (С) можно представить как
, (2.6)
где З- затраты; VВП- объем валовой продукции.
Общую сумму затрат можно заменить отдельными элементами: оплата труда (ОТ), сырье и материалы (СМ), амортизация (А), накладные расходы (Н)- и представить модель как
, (2.7)
где Х1- трудоемкость продукции; Х2- материалоемкость продукции;
Х3- фондоемкость продукции; Х4- уровень накладных расходов.
Способ формального разложения предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей.
Например: показатель рентабельности производства можно представить как отношение прибыли от реализации продукции к затратам.
Если сумму затрат заменить на отдельные ее элементы, то конечная модель в результате преобразования примет следующий вид:
, (2.8)
. (2.9)
Метод расширения представляет расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей.
Например:
, (2.10)
т.е. в результате получилась конечная мультипликативная модель в виде произведения нового набора факторов
, (2.11)
где ГВ - среднегодовая выработка;
SД - количество отработанных дней всеми работниками;
Ч - численность работников,
ДВ – дневная выработка;
Д – количество отработанных дней одним работником.
Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель.
|
|
Например:
. (2.12)
Экономическая рентабельность предприятия определяется делением суммы прибыли (П) на среднегодовую стоимость основного и оборотного капитала предприятия (К). Если числитель и знаменатель дроби разделить на объем товарооборота (РП), то получится кратная модель, но с новым набором факторов: рентабельности реализованной продукции (ReРП) и капиталоемкости продукции (КеП):
. (2.13)
В общем виде детерминированную модель можно представить в виде функции нескольких переменных:
Y = f (x1, x2,…,xi, …xn). (2.14)
Задача детерминированного факторного анализа заключается в определении или количественной оценке влияния каждого фактора на результативный показатель.
Наиболее часто из всех способов детерминированного факторного анализа применяется способ цепных подстановок, основанный на элиминировании. Элиминировать – значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. При этом исходят из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения, потом изменяются два при неизменности других и так далее.